题目内容
5.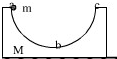 如图所示,物块M内部有一光滑半球,质量为m的小球从半球左端与圆心等高处由静止释放到运动到最低点的过程中,M始终静止于水平地面上,下列说法中不正确的是( )
如图所示,物块M内部有一光滑半球,质量为m的小球从半球左端与圆心等高处由静止释放到运动到最低点的过程中,M始终静止于水平地面上,下列说法中不正确的是( )| A. | 小球所受重力功率先增大后减小 | |
| B. | 小球运动到最低点时,地面对M的支持力大小为(M+3m)g | |
| C. | 地面对M的摩擦力一直增大 | |
| D. | 地面对M的支持力一直增大 |
分析 重力功率P=mgvy,vy是竖直分速度,运用特殊值法判断.根据机械能守恒和牛顿第二定律求小球运动到最低点时地面对M的支持力.对小球和半球受力分析,根据牛顿第二定律列式分析地面对滑块的摩擦力和支持力的情况.
解答 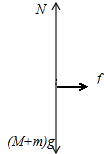 解:A、小球重力的功率等于重力和重力方向的分速度的乘积,即P=mgvy,vy是竖直分速度,由于最低点速度水平,竖直方向的分速度为零,此时重力的瞬时功率为零.刚释放时重力功率也为零.故小球下滑到最低点的过程中,竖直方向的分速度先增大,后减小,故重力的瞬时功率先增大后减小,故A正确;
解:A、小球重力的功率等于重力和重力方向的分速度的乘积,即P=mgvy,vy是竖直分速度,由于最低点速度水平,竖直方向的分速度为零,此时重力的瞬时功率为零.刚释放时重力功率也为零.故小球下滑到最低点的过程中,竖直方向的分速度先增大,后减小,故重力的瞬时功率先增大后减小,故A正确;
B、设小球到最低点时速度大小为v,则由机械能守恒得:mgR=$\frac{1}{2}m{v}^{2}$
小球运动到最低点时,由牛顿第二定律得:N-mg=m$\frac{{v}^{2}}{R}$,联立得 N=3mg,由牛顿第三定律得知小球对半球的压力大小为3mg,以半球为研究对象,可知地面对M的支持力大小为(M+3m)g,故B正确.
C、小球运动到最低点时,水平方向不受外力,小球对半球水平方向没有作用力,则半球没有运动趋势,此时M不受静摩擦力,可知地面对M的摩擦力不可能一直增大,故C错误.
D、对整体受力分析,受到重力、支持力和向右的静摩擦力,如图,根据牛顿第二定律,有
N-(M+m)g=may
解得N=(M+m)g+may,ay是小球竖直分加速度,小球加速下滑,ay增大,N增大,即地面对M的支持力一直增大,故D正确.
本题选不正确的,故选:C.
点评 本题关键对小球和半球整体或滑块受力分析,然后根据牛顿第二定律或共点力平衡条件列式分析.对于加速度不同的物体系统,也可以运用整体法,牛顿第二定律公式可变成:x方向:Fx合=m1a1x+m2a2x+…;y方向:Fy合=m1a1y+m2a2y+…,可尝试运用.


(2)在描绘该小灯泡的伏安特性曲线时,将(1)中的小灯泡接入如图2所示的电路进行实验,得到如表的数据,请在所给图3的坐标系中描绘出小灯泡的伏安特性曲线;
| U/V | 0.0 | 0.2 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| I/A | 0.000 | 0.050 | 0.100 | 0.150 | 0.180 | 0.195 | 0.205 | 0.215 |
| A. | 气体如果失去了容器的约束就会散开,这是因为气体分子之间存在势能的缘故 | |
| B. | 一定量100℃的水变成100℃的水蒸气,其分子之间的势能增加 | |
| C. | 一定量气体的内能等于其所有分子热运动动能和分子之间势能的总和 | |
| D. | 如果气体温度升高,那么所有分子的速率都增加 | |
| E. | 如果气体温度升高,那么分子的平均动能增加 |
A.电压表V1:量程3V,内阻约为2kΩ
B.电压表V2:量程10V,内阻为5kΩ
C.电源E:电动势约为10V,内阻不计
D.滑动变阻器R:最大阻值为20Ω
E.定值电阻R1:阻值5kΩ
F.定值电阻R2:阻值30kΩ
G.电键S及导线若干

该同学设计了如图甲所示的实验电路图,通过改变滑动变阻器R的阻值,测量多组电压表V1的读数U1和电压表V2的读数U2,最终求出了电压表V1的内阻.
(1)实验中定值电阻应选用R1(填字母代号);
(2)该同学在实验中测得数据如表:请在图乙的坐标中,描点作出U1-U2的图象.
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| U1/V | 0.50 | 0.90 | 1.30 | 1.70 | 2.00 | 2.30 | 2.50 |
| U2/V | 1.89 | 3.40 | 4.91 | 6.42 | 7.56 | 8.69 | 9.44 |
| A. | 电容器放电完毕时,电容器中的电场能为零,电路中电流为零 | |
| B. | 电容器充电完毕时,线圈中的磁场能为零,电路中电流为零 | |
| C. | 电容器放电过程中,振荡电流一定不断减小 | |
| D. | 电容器充电过程中,振荡电流一定不断增大 |
 如图1所示,螺线管内有平行于轴线的匀强磁场,规定图中箭头所示方向为磁感应强度B的正方向,螺线管与U型导线框cdef相连,导线框cdef内有一半径很小的金属圆环L,圆环与导线框cdef在同一平面内.当螺线管内的磁感应强度随时间按图2所示规律变化时( )
如图1所示,螺线管内有平行于轴线的匀强磁场,规定图中箭头所示方向为磁感应强度B的正方向,螺线管与U型导线框cdef相连,导线框cdef内有一半径很小的金属圆环L,圆环与导线框cdef在同一平面内.当螺线管内的磁感应强度随时间按图2所示规律变化时( )| A. | 在t1时刻,导线框cdef内的感应电流最大 | |
| B. | 在t2时刻,导线框cdef内的感应电流最大 | |
| C. | 在t1-t2时间内,金属圆环L内有顺时针方向的感应电流 | |
| D. | 在t1-t2时间内,金属圆环L有收缩趋势 |

 如图甲所示,光滑导轨宽0.4m,ab为金属棒,均匀变化的磁场垂直穿过轨道平面,磁场的变化情况如图乙所示,金属棒ab的电阻为1Ω,导轨电阻不计.t=0时刻,ab棒从导轨最左端,以v=1m/s的速度向右匀速运动,求1s末回路中的感应电流及金属棒ab受到的安培力.
如图甲所示,光滑导轨宽0.4m,ab为金属棒,均匀变化的磁场垂直穿过轨道平面,磁场的变化情况如图乙所示,金属棒ab的电阻为1Ω,导轨电阻不计.t=0时刻,ab棒从导轨最左端,以v=1m/s的速度向右匀速运动,求1s末回路中的感应电流及金属棒ab受到的安培力.