题目内容
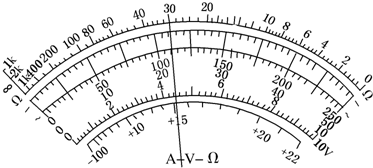
1.利用电磁打点计时器测定匀加速直线运动的小车的加速度,所使用的交流电源频率为50Hz.如图给出了该次实验中得到的纸带,从0点开始,每两个计数点间有四个计时点未画出,1、2、3、4、5、6均为计数点,测得S1=1.40cm,S2=1.90cm,S3=2.38cm,S4=2.88cm,S5=3.39cm,S6=3.87cm,
(1)在计时器打出点1、2、3、4、5时,小车的速度分别为:v1=0.165m/s,v2=0.214m/s,v3=0.263m/s,v4=0.314m/s,v5=0.363m/s.(计算结果保留3位有效数字)
(2)由题中给出的数据求出小车的加速度a=0.496m/s2.(计算结果保留3位有效数字)
分析 根据某段时间内的平均速度等于中间时刻的瞬时速度求出计数点1、2、3、4、5点的瞬时速度,根据连续相等时间内的位移之差是一恒量,运用逐差法求出加速度.
解答 解:(1)计数点1的瞬时速度${v}_{1}=\frac{{s}_{1}+{s}_{2}}{2T}=\frac{(1.40+1.90)×1{0}^{-2}}{0.2}$m/s=0.165m/s,计数点2的瞬时速度${v}_{2}=\frac{{s}_{2}+{s}_{3}}{2T}=\frac{(1.90+2.38)×1{0}^{-2}}{0.2}$m/s=0.214m/s,
计数点3的瞬时速度${v}_{3}=\frac{{s}_{3}+{s}_{4}}{2T}=\frac{(2.38+2.88)×1{0}^{-2}}{0.2}$m/s=0.263m/s,计数点4的瞬时速度${v}_{4}=\frac{{s}_{4}+{s}_{5}}{2T}=\frac{(2.88+3.39)×1{0}^{-2}}{0.2}$m/s=0.314m/s,
计数点5的瞬时速度${v}_{5}=\frac{{s}_{5}+{s}_{6}}{2T}=\frac{(3.39+3.87)×1{0}^{-2}}{0.2}$m/s=0.363m/s.
(2)根据△x=aT2,运用逐差法得,a=$\frac{{s}_{4}+{s}_{5}+{s}_{6}-{s}_{1}-{s}_{2}-{s}_{3}}{9{T}^{2}}$=$\frac{(2.88+3.39+3.87-1.40-1.90-2.38)×1{0}^{-2}}{9×0.01}$=0.496m/s2
故答案为:(1)0.165,0.214,0.263,0.314,0.363.
(2)0.496.
点评 解决本题的关键掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,关键是匀变速直线运动推论的运用.

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案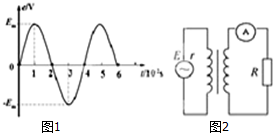 如图1所示,理想变压器输入端接在电动势随时间变化,内阻为r的交流电源上,输出端接在理想电流表及阻值为R的负载,变压器原副线圈匝数比值为$\sqrt{r}:\sqrt{R}$;如果要求负载上消耗的电功率最大,则下列说法正确的是( )
如图1所示,理想变压器输入端接在电动势随时间变化,内阻为r的交流电源上,输出端接在理想电流表及阻值为R的负载,变压器原副线圈匝数比值为$\sqrt{r}:\sqrt{R}$;如果要求负载上消耗的电功率最大,则下列说法正确的是( )| A. | 交流电源的效率为50% | |
| B. | 电流表的读数为$\frac{E_m}{{2\sqrt{2}Rr}}$ | |
| C. | 负载上消耗的热功率为$\frac{{E}_{m}^{2}}{4r}$ | |
| D. | 该交流电源电动势的瞬时表达式为e=Emsin(100πt) |
| A. | 树枝在风的作用下运动 | B. | 竖直向上抛出的物体的运动 | ||
| C. | 说话时声带的运动 | D. | 爆炸声引起窗扇的运动 |
 如图所示是观察水面波衍射的实验装置,AC和BD是两块挡板,AB是一个孔,O是波源,图中已画出波源所在区域波的传播情况,每两条相邻波纹(图中曲线)之间距离表示一个波长,则波经过孔之后的传播情况,下列描述正确的是 ( )
如图所示是观察水面波衍射的实验装置,AC和BD是两块挡板,AB是一个孔,O是波源,图中已画出波源所在区域波的传播情况,每两条相邻波纹(图中曲线)之间距离表示一个波长,则波经过孔之后的传播情况,下列描述正确的是 ( )| A. | 此时能明显观察到波的衍射现象 | |
| B. | 挡板前后波纹间距离相等 | |
| C. | 如果将孔AB扩大,有可能观察不到明显的衍射现象 | |
| D. | 如果孔的大小不变,使波源频率增大,能更明显地观察到衍射现象 | |
| E. | 挡板前后波纹间距离不等 |
| A. | 使用弹簧测力计前应将测力计水平放置,然后检查并矫正零点 | |
| B. | 用弹簧测力计拉细绳套时,拉力应沿弹簧的轴线,且与水平木板平行 | |
| C. | 两细绳套必须等长 | |
| D. | 用弹簧测力计拉细绳套时,拉力应适当大些,但不能超过量程 | |
| E. | 在实验中,如果只将细绳换成橡皮筋,其它步骤没有改变,那么实验结果会发生变化 |
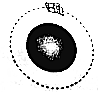 北斗卫星导航系统是中国自主发展、独立运行的全球卫星导航系统,北斗卫星导航系统由空间段、地面段和用户段三部分组成,空间段包括5颗静止轨道卫星和30颗非静止轨道卫星,假设一颗非静止轨道卫星a在轨道上绕行n圈所用时间为t,如图所示,已知地球的半径为R,地球表面处的重力加速度为g,引力常量为G,求:
北斗卫星导航系统是中国自主发展、独立运行的全球卫星导航系统,北斗卫星导航系统由空间段、地面段和用户段三部分组成,空间段包括5颗静止轨道卫星和30颗非静止轨道卫星,假设一颗非静止轨道卫星a在轨道上绕行n圈所用时间为t,如图所示,已知地球的半径为R,地球表面处的重力加速度为g,引力常量为G,求: