题目内容
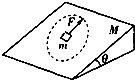
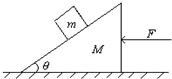 一质量为M,倾角为θ的楔形木块,静置在水平桌面上,与桌面间的滑动摩擦系数为μ.一质量为m的物块,置于楔形木块的斜面上,物块与斜面的接触是光滑的.为了保持物块相对斜面静止,可用一水平力F推楔形木块,如图所示.求水平力F的大小等于多少?
一质量为M,倾角为θ的楔形木块,静置在水平桌面上,与桌面间的滑动摩擦系数为μ.一质量为m的物块,置于楔形木块的斜面上,物块与斜面的接触是光滑的.为了保持物块相对斜面静止,可用一水平力F推楔形木块,如图所示.求水平力F的大小等于多少?
解:先对m进行研究,受重力mg,斜面支持力N,如图
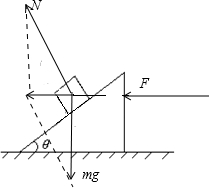
由于M和m一起向左加速而相对静止,则mg与N合力向左,且合力等于ma.
如图,由数学知识可知
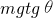 =
=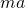
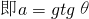
再对m和M整体研究
在竖直方向是平衡状态,受重力(M+m)g,受地面支持力FN,且FN=(M+m)g.
水平方向向左匀加速运动,受向左推力F和向右滑动摩擦力f,根据牛顿第二定律,有
F-f=(M+m)a
由于
f=μ(M+m)g
将a代入,得

故水平力F的大小等于(m+M)g?tgθ+μ(m+M)g.
分析:先对滑块受力分析,然后根据牛顿第二定律并运用合成法求出加速度;再对整体受力分析,根据牛顿第二定律求解出推力F.
点评:本题关键先对滑块受力分析后运用牛顿第二定律求出加速度,再对整体受力分析后运用牛顿第二定律求解推力F.

由于M和m一起向左加速而相对静止,则mg与N合力向左,且合力等于ma.
如图,由数学知识可知
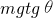 =
=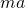
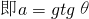
再对m和M整体研究
在竖直方向是平衡状态,受重力(M+m)g,受地面支持力FN,且FN=(M+m)g.
水平方向向左匀加速运动,受向左推力F和向右滑动摩擦力f,根据牛顿第二定律,有
F-f=(M+m)a
由于
f=μ(M+m)g
将a代入,得

故水平力F的大小等于(m+M)g?tgθ+μ(m+M)g.
分析:先对滑块受力分析,然后根据牛顿第二定律并运用合成法求出加速度;再对整体受力分析,根据牛顿第二定律求解出推力F.
点评:本题关键先对滑块受力分析后运用牛顿第二定律求出加速度,再对整体受力分析后运用牛顿第二定律求解推力F.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,质量为M、倾角为θ的斜劈形物体固定在水平地面上,质量为m的物块与斜面之间的动摩擦因素为μ.并以某一初速度沿劈的斜面向上滑,至速度为零后静止在斜面上,而斜劈始终保持静止.则下列选项中正确的是( )
如图所示,质量为M、倾角为θ的斜劈形物体固定在水平地面上,质量为m的物块与斜面之间的动摩擦因素为μ.并以某一初速度沿劈的斜面向上滑,至速度为零后静止在斜面上,而斜劈始终保持静止.则下列选项中正确的是( ) (2008?湖北模拟)一质量为M、倾角为θ的斜面体放在水平地面上,质量为m的小木块(可视为质点)放在斜面上,现用一平行于斜面、大小恒定的拉力F作用于小木块,拉力在斜面所在的平面内绕小木块旋转一周的过程中,斜面体和木块始终保持静止状态,下列说法中正确的是( )
(2008?湖北模拟)一质量为M、倾角为θ的斜面体放在水平地面上,质量为m的小木块(可视为质点)放在斜面上,现用一平行于斜面、大小恒定的拉力F作用于小木块,拉力在斜面所在的平面内绕小木块旋转一周的过程中,斜面体和木块始终保持静止状态,下列说法中正确的是( ) 如图所示,放置在水平地面上的直角劈质量为M、倾角为θ,有一质量为m的物体在其上以加速度a匀加速下滑而直角劈仍保持静止,则直角劈对地面的压力为
如图所示,放置在水平地面上的直角劈质量为M、倾角为θ,有一质量为m的物体在其上以加速度a匀加速下滑而直角劈仍保持静止,则直角劈对地面的压力为