题目内容
19.跳伞运动员做跳伞表演,他离开飞机后先做自由落体运动,当距离地面高度为125m时打开降落伞,伞张开后运动员就以10m/s2的加速度做匀减速运动,到达地面时速度恰好为0,(假设跳伞运动员只在竖直方向运动且g=10m/s2)问:(1)运动员离开飞机时距地面的高度为多少?
(2)离开飞机后,经过所长时间到达地面?
分析 根据匀变速直线运动的速度位移公式求出匀减速运动的初速度,结合速度位移公式求出自由落体运动的高度,从而得出运动员离开飞机时距离地面的高度.
解答 解:(1)根据匀变速直线运动的速度位移公式得:
${v}^{2}-{{v}_{0}}^{2}=-2ax$,
代入数据解得:v0=50m/s,
自由落体运动的高度为:${h}_{1}=\frac{{{v}_{0}}^{2}}{2g}=\frac{2500}{20}m=125m$,
则运动员离开飞机时距地面的高度为:H=h1+x=125+125m=250m.
(2)自由落体运动的时间为:${t}_{1}=\frac{{v}_{0}}{g}=\frac{50}{10}s=5s$,
匀减速直线运动的时间为:${t}_{2}=\frac{0-{v}_{0}}{a}=\frac{-50}{-10}s=5s$,
则下落的总时间为:t=t1+t2=5+5s=10s.
答:(1)运动员离开飞机时距地面的高度为250m;
(2)离开飞机后,经过10s时间到达地面.
点评 解决本题的关键理清运动员整个过程中的运动规律,结合速度位移公式求出自由落体运动的末速度是关键.

练习册系列答案
相关题目
10. 放射性同位素14C在考古中有重要应用.为研究14C的衰变规律,将一个原来静止的14C原子核放在匀强磁场中,观察到它所放射的粒子与反冲核的径迹是两个内切的圆,圆的半径之比R:r=7:1,如图所示,那么14C的衰变方程式应是( )
放射性同位素14C在考古中有重要应用.为研究14C的衰变规律,将一个原来静止的14C原子核放在匀强磁场中,观察到它所放射的粒子与反冲核的径迹是两个内切的圆,圆的半径之比R:r=7:1,如图所示,那么14C的衰变方程式应是( )
 放射性同位素14C在考古中有重要应用.为研究14C的衰变规律,将一个原来静止的14C原子核放在匀强磁场中,观察到它所放射的粒子与反冲核的径迹是两个内切的圆,圆的半径之比R:r=7:1,如图所示,那么14C的衰变方程式应是( )
放射性同位素14C在考古中有重要应用.为研究14C的衰变规律,将一个原来静止的14C原子核放在匀强磁场中,观察到它所放射的粒子与反冲核的径迹是两个内切的圆,圆的半径之比R:r=7:1,如图所示,那么14C的衰变方程式应是( )| A. | ${\;}_{6}^{14}$C→${\;}_{4}^{10}$Be+${\;}_{2}^{4}$He | B. | ${\;}_{6}^{14}$C→${\;}_{5}^{14}$B+${\;}_{1}^{0}$e | ||
| C. | ${\;}_{6}^{14}$C→${\;}_{7}^{14}$N+${\;}_{-1}^{0}$e | D. | ${\;}_{6}^{14}$C→${\;}_{5}^{12}$B+${\;}_{1}^{2}$H |
7.一个电荷量为10-6C的负电荷从电场中A点移到B点,电场力做功2×10-6J,从C点到D点克服电场力做功7×10-6J,已知C点电势比B点高3V,D点电势为0,则( )
| A. | A点的电势为4V | |
| B. | 电荷在B点的电势能为4×10-6J | |
| C. | 电荷从D移到B克服电场力做功4×10-6J | |
| D. | C、A点间电势差UCA为5V |
11.物体在共点力作用下,下列说法中正确的是( )
| A. | 物体的速度在某一时刻等于零时,物体就一定处于平衡状态 | |
| B. | 物体处于平衡状态,就一定是静止的 | |
| C. | 物体所受合力为零时,就一定处于平衡状态 | |
| D. | 物体做匀加速直线运动时,物体处于平衡状态 |
8.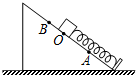 如图所示,斜面固定在水平面上,轻质弹簧一端固定在斜面底端,另一端与小物块相连,弹簧处于自然长度时物块位于O点,物块与斜面间有摩擦.现将物块从O点推至A点,撤去推力后物块由静止向上运动,经O点到达B点时速度为零,则物块从A运动到B的过程中( )
如图所示,斜面固定在水平面上,轻质弹簧一端固定在斜面底端,另一端与小物块相连,弹簧处于自然长度时物块位于O点,物块与斜面间有摩擦.现将物块从O点推至A点,撤去推力后物块由静止向上运动,经O点到达B点时速度为零,则物块从A运动到B的过程中( )
 如图所示,斜面固定在水平面上,轻质弹簧一端固定在斜面底端,另一端与小物块相连,弹簧处于自然长度时物块位于O点,物块与斜面间有摩擦.现将物块从O点推至A点,撤去推力后物块由静止向上运动,经O点到达B点时速度为零,则物块从A运动到B的过程中( )
如图所示,斜面固定在水平面上,轻质弹簧一端固定在斜面底端,另一端与小物块相连,弹簧处于自然长度时物块位于O点,物块与斜面间有摩擦.现将物块从O点推至A点,撤去推力后物块由静止向上运动,经O点到达B点时速度为零,则物块从A运动到B的过程中( )| A. | 从A运动到O的过程,物块一直做加速运动 | |
| B. | 增大A、O间的距离,物块动能最大的位置保持不变 | |
| C. | 物块从A向O运动过程中,弹力做功等于物块机械能的增加量 | |
| D. | 物块从O向B运动过程中,动能的减少量等于弹性势能和重力势能的增加量 |
 2015年省锡中运动会已圆满落下帷幕.期间摄影组同学运用了如图所示四旋翼无人机拍下了精彩的运动会实况.它是一种能垂直起降的遥控飞行器,已知某品牌的无人机质量m=2kg,其动力系统能使它产生向上的加速度.
2015年省锡中运动会已圆满落下帷幕.期间摄影组同学运用了如图所示四旋翼无人机拍下了精彩的运动会实况.它是一种能垂直起降的遥控飞行器,已知某品牌的无人机质量m=2kg,其动力系统能使它产生向上的加速度.