题目内容
 在如图所示的直角坐标系中,第一象限内存在着一个水平宽度为L(ON>L≥
在如图所示的直角坐标系中,第一象限内存在着一个水平宽度为L(ON>L≥| ON |
| 2 |
2
| ||
| 3 |
(1)磁感应强度B1的大小和磁场B1左边界距Y轴的距离.
(2)电场强度E的大小.
(3)电子从P点,第一次到达坐标原点O所经历的时间t.
分析:(1)作出粒子运动的轨迹图,结合几何关系求出半径的大小,根据洛伦兹力提供向心力求出磁感应强度B1的大小,结合几何关系求出B1左边界距y轴距离.
(2)电子在电场中做类平抛运动,结合沿电场方向和垂直电场方向上的运动规律求出电场强度的大小.
(3)根据平行四边形定则得出电子出电场后进入第三象限时的速度方向,结合几何关系得出圆心角的大小,根据周期公式求出电子从P点,第一次到达坐标原点O所经历的时间.
(2)电子在电场中做类平抛运动,结合沿电场方向和垂直电场方向上的运动规律求出电场强度的大小.
(3)根据平行四边形定则得出电子出电场后进入第三象限时的速度方向,结合几何关系得出圆心角的大小,根据周期公式求出电子从P点,第一次到达坐标原点O所经历的时间.
解答:解:(1)如图所示,设H为匀强磁场B1的左边界上的一点,做0H垂直于V.,有:OH=OMcos30°=
bcos30°=b ①
由于0N、OH垂直于V0,所以粒子在磁场B1中以O为圆心做匀速圆周运动,轨道半径:R=OH=h ②
由m
=eB1v0…③
得:R=
…④
故得:B1=
…⑤
设B1左边界距y轴距离为d,则
d=bcos60°=
…⑥
(2)电子在电场中做类平抛运动,有:v0t=OP=2b得
t=
…⑦
b=
t2…⑧
解得.E=
…⑨
(3)tanα=
=
,代入E、t的值得α=45…⑩
电子在磁场B2中以0′为圆心做匀速圆周,圆心角为2700,运动的时间为:t′=
T
而T=
,可求得:t′=
答:(1)磁感应强度B1的大小B1=
.磁场B1左边界距Y轴的距离为
.
(2)电场强度E的大小为E=
.
(3)电子从P点,第一次到达坐标原点O所经历的时间t′=
.
2
| ||
| 3 |
由于0N、OH垂直于V0,所以粒子在磁场B1中以O为圆心做匀速圆周运动,轨道半径:R=OH=h ②
由m
| ||
| R |
得:R=
| mv0 |
| eB1 |
故得:B1=
| mv0 |
| eb |
设B1左边界距y轴距离为d,则
d=bcos60°=
| b |
| 2 |
(2)电子在电场中做类平抛运动,有:v0t=OP=2b得
t=
| 2b |
| v0 |
b=
| 1 |
| 2 |
| eE |
| m |
解得.E=
m
| ||
| 2eb |

(3)tanα=
| v0 |
| vx |
| v0 | ||
|
电子在磁场B2中以0′为圆心做匀速圆周,圆心角为2700,运动的时间为:t′=
| 3 |
| 4 |
而T=
| 2πm |
| eB2 |
| 3πm |
| 2eB2 |
答:(1)磁感应强度B1的大小B1=
| mv0 |
| eb |
| b |
| 2 |
(2)电场强度E的大小为E=
m
| ||
| 2eb |
(3)电子从P点,第一次到达坐标原点O所经历的时间t′=
| 3πm |
| 2eB2 |
点评:解决本题的关键理清粒子在复合场中的运动情况,画出轨迹图,结合几何关系,运用在磁场中运动的半径公式、周期公式,在电场中做类平抛运动的运动学公式进行求解.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 在如图所示的直角坐标中,x轴的上方有与x轴正方向成45°角的匀强电场,场强的大小为E=
在如图所示的直角坐标中,x轴的上方有与x轴正方向成45°角的匀强电场,场强的大小为E= (2008?济宁一模)在如图所示的直角坐标中,x轴的上方有与x轴正方向成45°角的匀强电场,场强的大小为E=
(2008?济宁一模)在如图所示的直角坐标中,x轴的上方有与x轴正方向成45°角的匀强电场,场强的大小为E=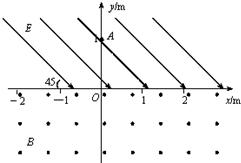 在如图所示的直角坐标中,x轴的上方有与x轴正方向成45°角的匀强电场,场强的大小为E=
在如图所示的直角坐标中,x轴的上方有与x轴正方向成45°角的匀强电场,场强的大小为E= ×104V/m。x轴的下方有垂直于xOy面的匀强磁场,磁感应强度的大小为
B=1×10-2T。把一个比荷为
×104V/m。x轴的下方有垂直于xOy面的匀强磁场,磁感应强度的大小为
B=1×10-2T。把一个比荷为 C/kg的正电荷从y轴上坐标为(0,1)的A点处由静止释放。电荷所受的重力忽略不计,求:
C/kg的正电荷从y轴上坐标为(0,1)的A点处由静止释放。电荷所受的重力忽略不计,求: