题目内容
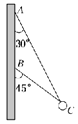
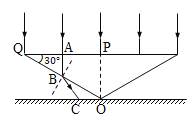
【题目】如图所示，在桌面上有一倒立的玻璃圆锥，其顶点O恰好与桌面接触，圆锥的轴线PO与桌面垂直，过轴线的截面为等腰三角形，底角为30°，腰长为a。有一与圆锥底面大小相同的圆柱形平行光束恰好全部垂直入射到圆锥的底面上。已知玻璃的折射率为
，真空中光速为c。求：
①由圆锥底面半径PQ中点A入射的光线，从A点到达桌面的传播时间；
②若保持圆锥玻璃位置不变，将桌面向下平移（桌面足够大），平移距离为多少时，桌面上会出现最小光斑，并计算其面积。
【答案】①
；②
【解析】
①光线从A点入射，不发生折射直接射到B点，在B点的入射角为
，因玻璃的折射率为
，由
故光线从B点折射出来至桌面上的C点，设B处折射角为
，根据
知
①
由几何关系得
AB=
，BC=
②
从A点入射至到达桌面经历的时间为
+ 
③
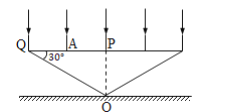
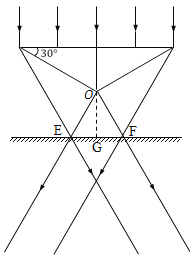
②如图所示，作出光路图
当桌面向下平移到图中EF位置时，桌面上光斑面积最小，已知腰长为a，根据几何关系知
为正三角形，则
，
，
④
故需要将桌面向下平移的距离为
⑤
桌面上光斑最小面积为以
为半径的圆面积
⑥
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
