题目内容
8.汽车以10m/s的速度在平直的公路上匀速行驶,司机突然发现前方2.7m处有一辆自行车正在以4m/s的速度做同方向的匀速直线运动,汽车司机立即鸣笛并且紧急制车,此时汽车的加速度大小为6m/s2,骑自行车人听到笛声立即加速前进,问骑自行车的人至少以多大的加速度加速才能避免车祸的发生?分析 抓住速度相等,结合速度时间公式求出两车速度相等时间的表达式,结合位移关系,根据运动学公式求出自行车的最小加速度.
解答 解:设自行车的最小加速度为a′,
速度相等时,有:v1-at=v2+a′t,解得t=$\frac{{v}_{1}-{v}_{2}}{a+a′}$=$\frac{6}{6+a′}$,
根据位移关系有:${v}_{1}t-\frac{1}{2}a{t}^{2}=2.7+{v}_{2}t+\frac{1}{2}a′{t}^{2}$,
代入数据解得a′=$\frac{2}{3}m/{s}^{2}$.
答:骑自行车的人至少以$\frac{2}{3}m/{s}^{2}$的加速度加速才能避免车祸的发生.
点评 本题考查了运动学中的追及问题,关键抓住临界状态,即速度相等时,恰好不相撞,结合运动学公式灵活求解.

练习册系列答案
相关题目
18.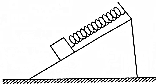 如图所示,一物块与弹簧连接叠放在粗糙斜面体上.两者始终相对静止.关于下列不同情况下对物块受力的判断正确的是( )
如图所示,一物块与弹簧连接叠放在粗糙斜面体上.两者始终相对静止.关于下列不同情况下对物块受力的判断正确的是( )
 如图所示,一物块与弹簧连接叠放在粗糙斜面体上.两者始终相对静止.关于下列不同情况下对物块受力的判断正确的是( )
如图所示,一物块与弹簧连接叠放在粗糙斜面体上.两者始终相对静止.关于下列不同情况下对物块受力的判断正确的是( )| A. | 若斜面体保持静止,则物块-定受到3个力 | |
| B. | 若斜面体向右匀速运动.则物块一定受到4个力 | |
| C. | 若斜面体向右加速运动,则物块可能受到4个力 | |
| D. | 若斜面体向左加速运动,则物块可能受到2个力 |
16.关于加速度的说法中正确的是( )
| A. | 加速度就是速度的增加量 | |
| B. | 加速度是矢量,其方向就是速度的方向 | |
| C. | 加速度越大,物体的速度变化也越大 | |
| D. | 加速度越大,物体的速度变化越快 |
17.关于速度、速度的改变量、加速度的关系,下列说法中不正确的是( )
| A. | 物体的速度不等于零,而加速度可能等于零 | |
| B. | 物体的速度改变量大,加速度就大 | |
| C. | 加速度越来越小,而速度可能越来越大 | |
| D. | 加速度不变,速度的变化量不一定为零 |
18. 如图所示,竖立在水平地面上的轻弹簧,下端与地面固定,将一个金属球放置在弹簧顶端(球与弹簧不相连),并用力向下压球,使弹簧在弹性限度内压缩,稳定后用细线把弹簧拴牢,烧断细线,球将被弹起,脱离弹簧后能继续向上运动,不计空气阻力,那么该球从细线被烧断到刚脱离弹簧的这一运动过程中( )
如图所示,竖立在水平地面上的轻弹簧,下端与地面固定,将一个金属球放置在弹簧顶端(球与弹簧不相连),并用力向下压球,使弹簧在弹性限度内压缩,稳定后用细线把弹簧拴牢,烧断细线,球将被弹起,脱离弹簧后能继续向上运动,不计空气阻力,那么该球从细线被烧断到刚脱离弹簧的这一运动过程中( )
 如图所示,竖立在水平地面上的轻弹簧,下端与地面固定,将一个金属球放置在弹簧顶端(球与弹簧不相连),并用力向下压球,使弹簧在弹性限度内压缩,稳定后用细线把弹簧拴牢,烧断细线,球将被弹起,脱离弹簧后能继续向上运动,不计空气阻力,那么该球从细线被烧断到刚脱离弹簧的这一运动过程中( )
如图所示,竖立在水平地面上的轻弹簧,下端与地面固定,将一个金属球放置在弹簧顶端(球与弹簧不相连),并用力向下压球,使弹簧在弹性限度内压缩,稳定后用细线把弹簧拴牢,烧断细线,球将被弹起,脱离弹簧后能继续向上运动,不计空气阻力,那么该球从细线被烧断到刚脱离弹簧的这一运动过程中( )| A. | 球所受弹力一定大于球的重力值 | |
| B. | 球刚脱离弹簧时的动能最大 | |
| C. | 在某一阶段内球的动能减小而它的机械能增加 | |
| D. | 地面对弹簧和球组成的系统不做功 |
 如图所示是某质点运动的v-t图象,请回答:
如图所示是某质点运动的v-t图象,请回答: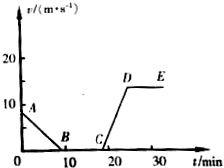 如图是一物体做直线运动的v-t图象,试问:AB、BC、CD、DE段各表示何种运动?在现实生活中,什么物体的运动大体可以用此图象来表示.
如图是一物体做直线运动的v-t图象,试问:AB、BC、CD、DE段各表示何种运动?在现实生活中,什么物体的运动大体可以用此图象来表示.