Question

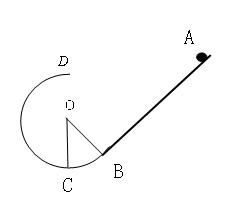
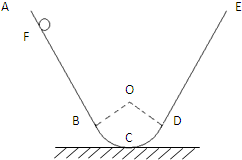
如图BCD为一半径为R的光滑圆弧面的一部分，C为圆弧的最低点，BD的连线与水平地面平行，∠BOD=106°，AB与圆弧BCD相切于B点，DE与圆弧BCD相切于D点．今将一质量为m的小物块（可视为质点）从F点由静止释放，已知FB两点间距离为5R，小物块与AB、DE间的动摩擦因数均为，当地的重力加速度为g．（取sin53°=，cos53°=）求：
（1）小物块第一次经过B点时的速度； 
（2）小物块第一次经过C点时对C点的压力；
（3）小物块在AB段和DE段经历的总路程之和．

Answer 1

【答案】分析：（1）对小物块在斜面上受力分析，利用力的平行四边形定则，确定摩擦力大小．再根据题意结合几何关系来确定斜面的倾角．最后小物块从F点运动到B点，由动能定理可求出小物块运动到B点的速度；
（2）由动能定理求出小物块运动到C点的速度大小，再由牛顿第二定律结合向心力公式可求出第一次经过C点时对C点的压力；
（3）小物块只有在AB与DE面上运动才有机械能损失，因此只有当小物块到达B点或D点的速度为零时，将只会在BCD间来回往复运动，且永不停息．所以由动能定理可求出小物块所经历的总路程．
解答：解：（1）由题意知，根据几何角度，可得斜面倾角为θ=53°
小物块，在斜面上，受力分析：重力G、支持力F、滑动摩擦力f，
由力的分解可得：f=μmgcosθ
从F到B，由动能定理
可得：mg×5R×sin53°-μmgcos53°×5R=
解之得：
（2）小物块，从B点到C点，由动能定理得
mg×（R-cos53°R）=         （1）
小物块，在C点，受力分析，
则有：F-mg=m                          （2）
由（1）（2）可联立解得：F=
（3）只有当小物块到达B点或D点的速度为零时，将只会在BCD间来回往复运动．
因而，小物块，从F点到B点（或D点），由动能定理，
则有：mg?5R×sin53°-μmgcos53°×L=0-0
解得：L=20R
答：（1）小物块第一次经过B点时的速度； 
（2）小物块第一次经过C点时对C点的压力mg；
（3）小物块在AB段和DE段经历的总路程之和为20R．
点评：考查动能定理，牛顿第二定律，向心力公式，并结合几何关系综合解题．值得注意：只有当小物块到达B点或D点速度为零时，才不会越上粗糙斜面．