题目内容
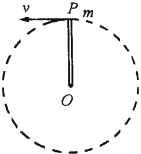如图所示，长度L=0.5m的轻质细杆OP，P端有一质量m=3.0kg的小球，小球以O点为圆心在竖直平面内做匀速圆周运动，其运动速率为2.0m/s，则小球通过最高点时杆OP所受的力为分析：根据牛顿第二定律求出小球在最高点杆子作用力为零时的速度，判断出杆子表现为拉力还是支持力．从而根据牛顿第二定律求出作用力的大小．
解答：解：小球以O点为圆心在竖直平面内作圆周运动，
当在最高点小球与细杆无弹力作用时，小球的速度为V1，则有
mg=m
得：v1=
=
m/s
∵
m/s＞2m/s∴小球受到细杆的支持力
小球在O点受力分析：重力与支持力
mg-F支=m
则F支=mg-m
=30-24=6N
故答案为：6
当在最高点小球与细杆无弹力作用时，小球的速度为V1，则有
mg=m
| v12 |
| L |
得：v1=
| gL |
| 5 |
∵
| 5 |
小球在O点受力分析：重力与支持力
mg-F支=m
| v22 |
| L |
则F支=mg-m
| v22 |
| L |
故答案为：6
点评：小球在杆的作用下做圆周运动，在最高点杆给球的作用是由小球的速度确定．因从球不受杆作用时的速度角度突破，比较两者的速度大小，从而确定杆给球的作用力．同时应用了牛顿第二、三定律．当然还可以假设杆给球的作用力，利用牛顿第二定律列式求解，当求出力是负值时，则说明假设的力与实际的力是方向相反．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
如图所示，长度L=0.50m的轻质杆OA，A端固定一个质量m=3.0kg的小球，小球以O为圆心在竖直平面内做圆周运动．通过最高点b时小球的速率是2.0m/s，g取10m/s2，则此时细杆OA受到大小为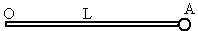
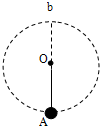如图所示，长度L=0.50m的轻质杆OA，A端固定一个质量m=3.0kg的小球，小球以O为圆心在竖直平面内做圆周运动．通过最高点b时小球的速率是2.0m/s，g取10m/s2，则此时细杆OA受到大小为________N的________力（填压力或拉力）