题目内容
【题目】如图所示，倾角为37°的斜面通过一小段光滑水平面BC与光滑竖直半圆形轨道CD相连，斜面和半圆形轨道固定在水平面上，C点和D点分别为半圆形轨道的最低点和最高点，一质量为m=1kg的滑块（可视为质点）从斜面的A点由静止开始下滑，经过半圆形轨道的最高点后垂直打在斜面的E点，已知E点与圆心O等高，滑块从A点运动到斜面低端B点所用的时间为t=3.2s，半圆形轨道的半径为R=0.8m，不计空气阻力，滑块通过B点时无能力损失， 
， 
， 
，求：
（1）滑块到达C点时对轨道的压力大小；
（2）滑块与斜面的动摩擦因数μ；
【答案】(1) 
(2) 
【解析】（1）滑块从D→E物体做平抛运动，有： 
①
分解E点的速度如图
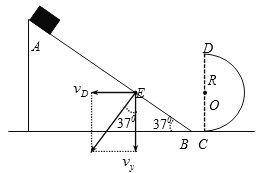
可得： 
② 又因： 
③
滑块从C→D过程，由机械能守恒得： 
④
滑块经过C点时，由牛顿第二定律得： 
⑤
联立解①②③④⑤式得： 
由牛顿第三定律得，滑块对轨道的压力大小为
（2）物体由A→B过程为匀加速直线运动（B点和C点的速度大小相等）
有： 
⑥，
⑦
由⑥⑦式得： 
练习册系列答案
相关题目
