题目内容
4. 如图,静止在光滑水平面上的A、B两物体,质量mA>mB,用大小相等、方向相反的两个水平外力分别对A、B作用相等距离,撤去两外力后A、B两物体相碰并粘在一起,此时两物体将( )
如图,静止在光滑水平面上的A、B两物体,质量mA>mB,用大小相等、方向相反的两个水平外力分别对A、B作用相等距离,撤去两外力后A、B两物体相碰并粘在一起,此时两物体将( )| A. | 停止运动 | B. | 向右运动 | C. | 向左运动 | D. | 以上均有可能 |
分析 根据动能定理求出碰前A、B的速度,再根据动量守恒定律得出粘合体的速度,从而判断运动的方向.
解答 解:根据动能定理得,$Fs=\frac{1}{2}m{v}^{2}$,解得碰撞前A的速度大小${v}_{A}=\sqrt{\frac{2Fs}{{m}_{A}}}$,B的速度大小${v}_{B}=\sqrt{\frac{2Fs}{{m}_{B}}}$,
规定向右为正方向,根据动量守恒定律有:mBvB-mAvA=(mA+mB)v,
因为${m}_{B}{v}_{B}-{m}_{A}{v}_{A}=\sqrt{2{m}_{B}Fs}-\sqrt{2{m}_{A}Fs}$,因为mA>mB,则mBvB-mAvA<0.则v<0,两物体将向左运动.
故选:C.
点评 本题考查了动能定理和动量守恒定律的综合,难度中等,在运用动量守恒定律时,注意A、B碰前的速度相反.

练习册系列答案
相关题目
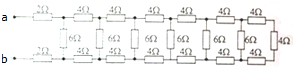
12. 如图所示,一导线弯成的闭合线圈(尺寸如图,右侧部分为半径为r的半圆),在纸面内以水平速度v向左匀速进入磁感应强度为B的匀强磁场,磁场方向垂直纸面向外.线圈总电阻为R,从线圈进入磁场开始到完全进入磁场为止,下列结论正确的是( )
如图所示,一导线弯成的闭合线圈(尺寸如图,右侧部分为半径为r的半圆),在纸面内以水平速度v向左匀速进入磁感应强度为B的匀强磁场,磁场方向垂直纸面向外.线圈总电阻为R,从线圈进入磁场开始到完全进入磁场为止,下列结论正确的是( )
 如图所示,一导线弯成的闭合线圈(尺寸如图,右侧部分为半径为r的半圆),在纸面内以水平速度v向左匀速进入磁感应强度为B的匀强磁场,磁场方向垂直纸面向外.线圈总电阻为R,从线圈进入磁场开始到完全进入磁场为止,下列结论正确的是( )
如图所示,一导线弯成的闭合线圈(尺寸如图,右侧部分为半径为r的半圆),在纸面内以水平速度v向左匀速进入磁感应强度为B的匀强磁场,磁场方向垂直纸面向外.线圈总电阻为R,从线圈进入磁场开始到完全进入磁场为止,下列结论正确的是( )| A. | 感应电流一直沿逆时针方向 | |
| B. | 线圈受到的安培力先增大,后减小 | |
| C. | 感应电动势的最大值E=Brv | |
| D. | 通过线圈某个横截面的电荷量为$\frac{{B({r^2}+π{r^2})}}{R}$ |
9.小球作类平抛运动时,分在两个互相垂直方向上的分运动的图线可能是( )


| A. | a和b | B. | b和d | C. | a和d | D. | c和d |
13.在地面附近某一高处水平抛出一物体,若不计空气阻力,则物体在空中的运动是( )
| A. | 匀变速运动 | B. | 变加速运动 | C. | 匀速率运动 | D. | 一段圆周运动 |
14.两行星运行轨迹的半长轴之比为4:9,其运行周期之比为( )
| A. | 4:9 | B. | 2:3 | C. | 8:27 | D. | 5:3 |
 一组太空人乘太空穿梭机去修理位于离地球表面6.0×105m的圆形轨道上的哈勃太空望远镜H.机组人员驾驶穿梭机S进入与H相同的轨道并关闭推动火箭,而望远镜在穿梭机前方数千米处,如图所示.引力常量为G,地球质量为ME(已知地球半径为R=6.4×106m,地球表面的重力加速度g=9.8m/s2)
一组太空人乘太空穿梭机去修理位于离地球表面6.0×105m的圆形轨道上的哈勃太空望远镜H.机组人员驾驶穿梭机S进入与H相同的轨道并关闭推动火箭,而望远镜在穿梭机前方数千米处,如图所示.引力常量为G,地球质量为ME(已知地球半径为R=6.4×106m,地球表面的重力加速度g=9.8m/s2)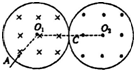 如图所示,在某空间实验室中,有两个靠在一起的等大的圆柱形区域.分别存在着等大反向的匀强磁场,磁感应强度B=0.10T,磁场区域半径r=$\frac{2}{3}\sqrt{3}m$,左侧区域圆心为O1,磁场向里,右侧区域圆心为O2,磁场向外.两区域切点为C.今有质量m=3.2×10-26 kg、带电荷量q=1.6×10-19 C的某种离子,从左侧区域边缘的A点以速度v=106m/s正对O1的方向垂直磁场射入,它将穿越C点后再从右侧区域穿出.求:
如图所示,在某空间实验室中,有两个靠在一起的等大的圆柱形区域.分别存在着等大反向的匀强磁场,磁感应强度B=0.10T,磁场区域半径r=$\frac{2}{3}\sqrt{3}m$,左侧区域圆心为O1,磁场向里,右侧区域圆心为O2,磁场向外.两区域切点为C.今有质量m=3.2×10-26 kg、带电荷量q=1.6×10-19 C的某种离子,从左侧区域边缘的A点以速度v=106m/s正对O1的方向垂直磁场射入,它将穿越C点后再从右侧区域穿出.求: 如图,放在水平地面上的瓶子质量为M,瓶中压缩气体密度为ρ,瓶口横截面积为S,地面与瓶间摩擦系数为μ,当打开瓶塞气体以速度v喷出时瓶子的加速度大小为多少?
如图,放在水平地面上的瓶子质量为M,瓶中压缩气体密度为ρ,瓶口横截面积为S,地面与瓶间摩擦系数为μ,当打开瓶塞气体以速度v喷出时瓶子的加速度大小为多少?