题目内容
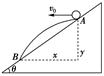
如图a所示,倾角为45°、高为h的斜面固定在水平地面上,小球从高为H(2h>H>h)的某处自由下落,与斜面碰撞(无能量损失)后做平抛运动。若小球做平抛运动后能直接落到水平地面上,自由下落的起始点距斜面左端的水平距离x应满足的条件是 (用符号表示);若测得x=1m时,小球平抛运动的水平射程s最大,且水平射程的平方s2与x关系如图b所示,则斜面的高h应为 m。

h>x>h-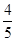 H,4
H,4
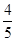 H,4
H,4试题分析:根据题述,h>x 。要使小球做平抛运动后能直接落到水平地面上,s>h-x,s=vt,h-x=
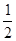 gt2,2g(H-h+x)=v2,联立解得x>h-
gt2,2g(H-h+x)=v2,联立解得x>h-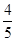 H,所以自由下落的起始点距斜面左端的水平距离x应满足的条件是h>x>h-
H,所以自由下落的起始点距斜面左端的水平距离x应满足的条件是h>x>h-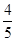 H。由图b可得射程s最大值s=6m,x=1m,代入s=vt,h-x=
H。由图b可得射程s最大值s=6m,x=1m,代入s=vt,h-x=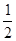 gt2,2g(H-h+x)=v2,联立解得s2=4(H-h+x)(h-x)=-4[(h-x)2-H(h-x)+H2/4]+ H2= -4[(h-x)-H/2]2 +H2。当(h-x)-H/2=0时,s2取最大值,s最大值为6m,对应的H=6m,斜面的高h=x+H/2=4m
gt2,2g(H-h+x)=v2,联立解得s2=4(H-h+x)(h-x)=-4[(h-x)2-H(h-x)+H2/4]+ H2= -4[(h-x)-H/2]2 +H2。当(h-x)-H/2=0时,s2取最大值,s最大值为6m,对应的H=6m,斜面的高h=x+H/2=4m点评:本题难度较小,平抛运动中注意小球落在斜面上的临界条件,合位移与分位移的关系

练习册系列答案
相关题目