题目内容
如图所示,一条轻质弹簧左端固定在水平桌面上,右端放一个可视为质点的小物块,小物块的质量为m=1.0 kg,当弹簧处于原长时,小物块静止于O点,现对小物块施加一个外力,使它缓慢移动,压缩弹簧(压缩量为x=0.1 m)至A点,在这一过程中,所用外力与压缩量的关系如图所示。然后释放小物块,让小物块沿桌面运动,已知O点至桌边B点的距离为L=2x。水平桌面的高为h=5.0 m,计算时,可用滑动摩擦力近似等于最大静摩擦力。(g取10 m/s2)
求:(1)在压缩弹簧过程中,弹簧存贮的最大弹性势能;
(2)小物块到达桌边B点时速度的大小;
(3)小物块落地点与桌边B的水平距离。
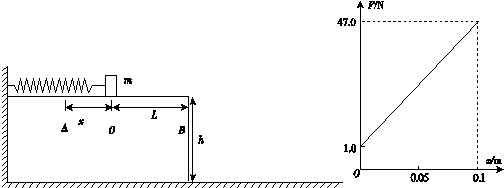
(1)从F-x图中看出,小物块与桌面的动摩擦力大小为f=1.0 N,在压缩过程中,摩擦力做功为Wf=f·x=-0.1 J(3分)
由图线与x轴所夹面积(如图),可得外力做功为
WF=(1+47)×0.1÷2=2.4 J (2分)
所以弹簧存贮的弹性势能为:EP=WF-Wf=2.3 J (2分)
(2)从A点开始到B点的过程中,由于L=2x,
摩擦力做功为W′f=f·3x=0.3 J (1分)
对小物块用动能定理有:
Ep+W fˊ=![]() mv
mv![]() (3分)
(3分)
解得:vB=2 m/s (2分)
(3)物块从B点开始做平抛运动h=![]() gt2 (2分)
gt2 (2分)
下落时间t=1 s (1分)
水平距离s=vBt=2 m (2分)
说明:用其他方法计算,如第(1)问用Ep=![]() kx2来计算,请参照上面给分办法相应给分。
kx2来计算,请参照上面给分办法相应给分。

 分享到
分享到- QQ空间
- 新浪微博
- 百度搜藏
- 人人网
- 腾讯微博
- 开心网
- 腾讯朋友
- 百度空间
- 豆瓣网
- 搜狐微博
- MSN
- QQ收藏
- 我的淘宝
- 百度贴吧
- 搜狐白社会
- 更多...
百度分享
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,用下面的方法测量它匀速转动时的角速度。
实验器材:电磁打点计时器、米尺、纸带、复写纸片。
实验步骤:
(1)如图1所示,将电磁打点计时器固定在桌面上,将纸带的一端穿过打点计时器的限位孔后,固定在待测圆盘的侧面上,使得圆盘转动时,纸带可以卷在圆盘侧面上。
(2)启动控制装置使圆盘转动,同时接通电源,打点计时器开始打点。
(3)经过一段时间,停止转动和打点,取下纸带,进行测量。
① 由已知量和测得量表示的角速度的表达式为ω= 。式中各量的意义是:
.
② 某次实验测得圆盘半径r=5.50×10-2m,得到纸带的一段如图2所示,求得角速度为 。
(1) (2)6.8/s。 |
