题目内容
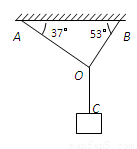
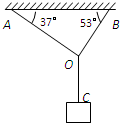 如图所示,轻绳AO、BO所能承受的最大拉力分别为Fm1=132N、Fm2=160N,轻绳OC能承受足够大拉力.它们一端固定在水平天花板上,在它们的结点O处用的悬吊一重物,绳AO、BO与天花板间的夹角分别为37°和53°.为保证绳均不断裂,重物的质量应不超过多少?
如图所示,轻绳AO、BO所能承受的最大拉力分别为Fm1=132N、Fm2=160N,轻绳OC能承受足够大拉力.它们一端固定在水平天花板上,在它们的结点O处用的悬吊一重物,绳AO、BO与天花板间的夹角分别为37°和53°.为保证绳均不断裂,重物的质量应不超过多少?(取g=10m/s2,sin37°=cos53°=0.6,cos37°=sin53°=0.8)
分析:以结点O为研究对象,将重物的拉力进行分析,假设在绳子均不被拉断的情况下,分别求出轻绳AO、BO所能承受的拉力达到最大时重物的质量,再确定重物的最大质量.
解答: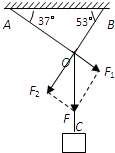 解:如图所示,当悬吊重物的质量为m时,绳AO所受拉力
解:如图所示,当悬吊重物的质量为m时,绳AO所受拉力
F1=Fsin37°=mgsin37°
绳BO所受拉力
F2=Fcos37°=mgcos37°
令F1=Fm1 即 mgsin37°=Fm1
得 m1=
=
=22(㎏)
令F2=Fm2 即 mgcos37°=Fm2
得 m2=
=
=20(㎏)
∴为保证绳均不断裂,重物的质量应不超过20㎏
答:为保证绳均不断裂,重物的质量应不超过20㎏.
 解:如图所示,当悬吊重物的质量为m时,绳AO所受拉力
解:如图所示,当悬吊重物的质量为m时,绳AO所受拉力F1=Fsin37°=mgsin37°
绳BO所受拉力
F2=Fcos37°=mgcos37°
令F1=Fm1 即 mgsin37°=Fm1
得 m1=
| Fm1 |
| gsin370 |
| 132 |
| 10×0.6 |
令F2=Fm2 即 mgcos37°=Fm2
得 m2=
| Fm2 |
| gcos370 |
| 160 |
| 10×0.8 |
∴为保证绳均不断裂,重物的质量应不超过20㎏
答:为保证绳均不断裂,重物的质量应不超过20㎏.
点评:本题是物体平衡中临界问题,采用的是假设法.其基础是分析物体受力、正确作出力的分解图.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
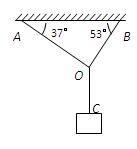
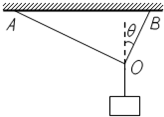 如图所示,轻绳AO和BO共同吊起质量为m的重物.AO与BO垂直,BO与竖直方向的夹角为θ.则( )
如图所示,轻绳AO和BO共同吊起质量为m的重物.AO与BO垂直,BO与竖直方向的夹角为θ.则( )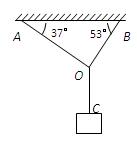
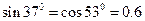 ,
,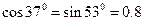 )
)
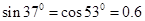 ,
,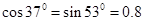 )
)