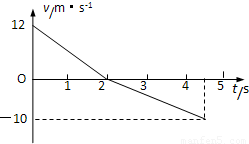
题目内容
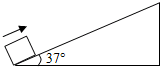 一物体以12m/s的初速度冲上一足够长斜面,然后又沿斜面向下运动,斜面倾角为37°,物体与斜面间的动摩擦因数为0.25,当地重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求
一物体以12m/s的初速度冲上一足够长斜面,然后又沿斜面向下运动,斜面倾角为37°,物体与斜面间的动摩擦因数为0.25,当地重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求(1)物体沿斜面向上运动的加速度大小;
(2)物体沿斜面向下运动的加速度大小;
(3)物体在斜面上向上运动和向下运动的时间之比为多少?
分析:(1)沿斜面向上运动时,由牛顿第二定律列式即可求解加速度的大小;
(2)沿斜面向下运动时,由牛顿第二定律列式即可求解加速度的大小;
(3)由于两次运动的位移大小相等,根据匀变速直线运动位移时间公式联立方程即可求解.
(2)沿斜面向下运动时,由牛顿第二定律列式即可求解加速度的大小;
(3)由于两次运动的位移大小相等,根据匀变速直线运动位移时间公式联立方程即可求解.
解答:解:(1)沿斜面向上运动时,由牛顿第二定律得:mgsinθ+μmgcosθ=ma1
代入数据解得:a1=8m/s2
(2)沿斜面向下运动,由牛顿第二定律得:mgsinθ-μmgcosθ=ma2
代入数据解得:a2=4m/s2
(3)由于两次运动的位移大小相等,则:
x=
a1
x=
a2
代入数据解得:
=
答:(1)物体沿斜面向上运动的加速度大小为8m/s2;
(2)物体沿斜面向下运动的加速度大小为4m/s2;
(3)物体在斜面上向上运动和向下运动的时间之比为1:
.
代入数据解得:a1=8m/s2
(2)沿斜面向下运动,由牛顿第二定律得:mgsinθ-μmgcosθ=ma2
代入数据解得:a2=4m/s2
(3)由于两次运动的位移大小相等,则:
x=
| 1 |
| 2 |
| t | 2 1 |
x=
| 1 |
| 2 |
| t | 2 2 |
代入数据解得:
| t1 |
| t2 |
| 1 | ||
|
答:(1)物体沿斜面向上运动的加速度大小为8m/s2;
(2)物体沿斜面向下运动的加速度大小为4m/s2;
(3)物体在斜面上向上运动和向下运动的时间之比为1:
| 2 |
点评:本题主要考查了牛顿第二定律及运动学基本公式的直接应用,注意上滑和下滑时摩擦力的方向,难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
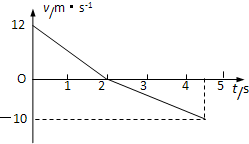 一物体以12m/s的初速度冲上斜面的最顶端,然后又沿斜面向下运动,返回斜
一物体以12m/s的初速度冲上斜面的最顶端,然后又沿斜面向下运动,返回斜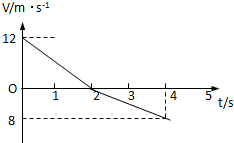 一物体以12m/s的初速度冲上斜面,然后又沿斜面向下运动,在此全过程中的v-t图象如图所示,求
一物体以12m/s的初速度冲上斜面,然后又沿斜面向下运动,在此全过程中的v-t图象如图所示,求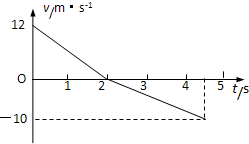 一物体以12m/s的初速度冲上斜面的最顶端,然后又沿斜面向下运动,返回斜
一物体以12m/s的初速度冲上斜面的最顶端,然后又沿斜面向下运动,返回斜