题目内容
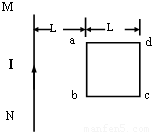
如图所示，有一通电直导线MN，其右侧有一边长为L的正方形线圈abcd，导线与线圈在同一平面内，且导线与ab边平行，距离为L．导线中通以如图方向的恒定电流，当线圈绕ab边沿逆时针方向（从上往下看）转过角度θ=120°
120°
时，穿过线圈中的磁通量Φ最小．分析：穿过线圈的磁通量由BS求得，当两者相平行时，磁通量最小，或穿过线圈后又穿回，则磁通量也最小．
解答：解：当直导线电流产生磁场的磁感线与线圈平面相切时，此时穿过线圈的磁通量最小，如图所示，（俯视图）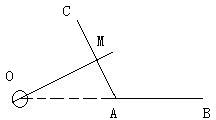
AC是AB转动后的位置．
根据几何关系，则有：OM⊥AC，OA=L AM=
，因此线圈绕ab边转过角度120°．
故答案为：120°．
AC是AB转动后的位置．
根据几何关系，则有：OM⊥AC，OA=L AM=
| L |
| 2 |
故答案为：120°．
点评：解决本题的关键是掌握磁通量的正负含义，并根据几何关系来应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
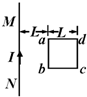
如图所示，有一通电直导线O垂直纸面放置，导线中电流方向垂直纸面向里，在其上方放一弓形硬质闭合线圈abcd，其圆弧的圆心恰好在通电直导线的O点上，当闭合线圈中通以逆时针方向电流时，线圈将（ ）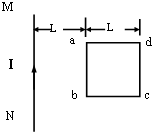
如图所示，有一通电直导线MN，其右侧有一边长为L的正方形线圈abcd，导线与线圈在同一平面内，且导线与ab边平行，距离为L．导线中通以如图方向的恒定电流，当线圈绕ab边沿逆时针方向（从上往下看）转过角度θ（θ＜90°）的过程中，线圈中产生感应电流的方向为
