题目内容
6.物体作匀加速直线运动,它在第3s内和第6s内的位移分别是2.2m和3.7m,则质点运动的加速度为0.5m/s2,前六秒内的平均速度为2.45m/s.分析 根据匀变速直线运动连续相等时间内的位移之差是一恒量求出质点的加速度,结合第3s内的位移,运用位移时间公式求出初速度.根据位移时间公式求出前6s内的位移,从而得出前6s内的平均速度.
解答 解:根据x6-x3=3at2,t=1s.
解得:a=$\frac{{x}_{6}-{x}_{3}}{3{t}^{2}}=\frac{3.7-2.2}{3}=0.5m/{s}^{2}$.
第3s内的位移为2.2m,有:2.2=v0t3+$\frac{1}{2}a{{t}_{3}}^{3}-{v}_{0}{t}_{2}-\frac{1}{2}a{{t}_{2}}^{2}$
代入时间得:v0=0.95m/s.
前6s内的位移为x=v0t+$\frac{1}{2}a{t}^{2}$=0.95×6+$\frac{1}{2}$×0.5×62=14.7m,
则前6s内的平均速度为:$\overline{v}=\frac{x}{t}=\frac{14.7}{6}=2.45$m/s
故答案为:0.5;2.45
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,有时运用推论求解会使问题更加简捷.

练习册系列答案
相关题目
16.以下情况中能反映物体做加速运动的是( )
| A. | v>0,a>0 | B. | v>0,a<0 | C. | v<0,a>0 | D. | v<0,a<0 |
1.2015年的股市经历了暴涨急跌,犹如过山车,目前在国家的积极救市下,正逐步回稳.如果将股价的“上涨”类比成运动学中的“加速”,将股价的“下跌”类比成运动学中的“减速”,你认为“股价下跌出现减缓趋势”可以类比成运动学中的( )
| A. | 速度增加,加速度减小 | B. | 速度增加,加速度增大 | ||
| C. | 速度减小,加速度减小 | D. | 速度减小,加速度增大 |
11. 如图所示,在x轴相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、$\frac{L}{2}$为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称.下列判断正确的是( )
如图所示,在x轴相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、$\frac{L}{2}$为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称.下列判断正确的是( )
 如图所示,在x轴相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、$\frac{L}{2}$为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称.下列判断正确的是( )
如图所示,在x轴相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、$\frac{L}{2}$为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称.下列判断正确的是( )| A. | b、d两点处的电势相等 | |
| B. | 四点中d点处的电势最低 | |
| C. | 将一试探电荷+q沿圆周由a点移至c点,+q的电势能减小 | |
| D. | b、d两点处的电场强度相同 |
12.如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在xOy平面的第一象限,存在以x轴、y轴及双曲线y=$\frac{{l}^{2}}{4x}$的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L为边界的匀强电场区域Ⅱ.两个电场强度的大小均为E,不计电子重力的影响,电子的电荷量为e,则以下说法中不正确的是( )
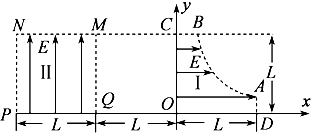

| A. | 从电场区域Ⅰ的边界B点(B点的纵坐标为L)处由静止释放电子,到达区域Ⅱ的M点时的速度为v=$\sqrt{\frac{eEL}{2m}}$ | |
| B. | 从电场区域Ⅰ的边界B(B点的极坐标为L)处由静止释放电子,电子离开MNPQ区域时的极坐标为(-2L,0) | |
| C. | 从电场区域Ⅰ的AB曲线上任一点处由静止释放的电子都能从MNPQ区域左下角P点离开 | |
| D. | 在电场区域Ⅰ的AB曲线上任一点处由静止释放的电子离开MNPQ区域时最小动能为2eEL |
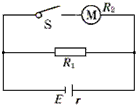 如图所示,直流电动机和电炉并联后接在直流电路上,电源的内阻r=1Ω,电炉的电阻R1=19Ω,电动机绕线的电阻R2=2Ω,当开关S断开时,电源内电路消耗的热功率P=25W;当闭合时,干路中的电流I=12.6A.求:
如图所示,直流电动机和电炉并联后接在直流电路上,电源的内阻r=1Ω,电炉的电阻R1=19Ω,电动机绕线的电阻R2=2Ω,当开关S断开时,电源内电路消耗的热功率P=25W;当闭合时,干路中的电流I=12.6A.求: