题目内容
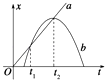
【题目】如图所示,倾角θ=30°的粗糙斜面上有四条间距相等的水平虚线MM'、NN'、PP'、QQ',在MM'与NN'之间、PP'与QQ'之间存在垂直斜面向下的匀强磁场,磁感应强度B均为1T。现有质量m=0.1kg、电阻R=4Ω的矩形线圈abcd,从图示位置静止释放(cd边与MM'重合),速度随时间的变化关系如图乙所示,t1时刻cd边与NN'重合,t2时刻ab边与PP'重合,t3时刻ab边与QQ'重合。已知矩形线框cd边长度L1=0.5 m,t1~t2的时间间隔![]() =1.2 s,线圈与斜面之间的动摩擦因数μ=
=1.2 s,线圈与斜面之间的动摩擦因数μ=![]() ,重力加速度g取10 m/s2。求:
,重力加速度g取10 m/s2。求:
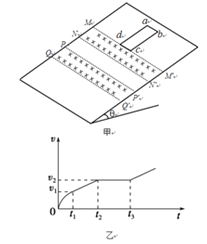
(1)线框匀速运动的速度v2的大小;
(2)磁场的宽度L0和线框ad边的长度L2;
(3)0~t3时间内,线圈产生的热量Q。
【答案】(1)![]()
(2)2m
(3)0.45J
【解析】
试题分析:(1)在t2时刻:ab棒切割磁感线:![]()
流过线圈的电流:![]()
根据线框匀速运动可得:![]()
解得:![]()
(2)由于t1~t2的时间线框匀加速运动,可知线圈ab边的长度是磁场宽度的2倍,即![]()
该过程中,根据牛顿第二定律![]()
![]()
根据线框的匀变速运动特点![]()
![]()
![]()
![]()
![]()
![]()
(3)根据能量守恒可得: ![]()

练习册系列答案
相关题目