��Ŀ����
����Ŀ����ͼ��ʾ��Ϊһ����װ�ã�����AB�δֲڣ�AB�γ�ΪL=0.2m����Ħ������![]() ��BC��DEN�ξ�����Ϊ�⻬����BC��ʼĩ�˾�ˮƽ������h=0.1m�ĸ߶ȲDEN�ǰ뾶Ϊr=0.4m�İ�Բ�ι������ֱ��DN����ֱ����Cλ��DN��ֱ���ϣ�CD��ľ���ǡ����С������ͨ�����������ֱǽ�Ϲ̶���һ���ʵ��ɣ�����һ����Ϊ�ʵ��С��С������m=0.2kg��ѹ�����ʵ�����A���ֹ�ͷţ�С��͵��ɲ��������С��պ�����DEN������£���
��BC��DEN�ξ�����Ϊ�⻬����BC��ʼĩ�˾�ˮƽ������h=0.1m�ĸ߶ȲDEN�ǰ뾶Ϊr=0.4m�İ�Բ�ι������ֱ��DN����ֱ����Cλ��DN��ֱ���ϣ�CD��ľ���ǡ����С������ͨ�����������ֱǽ�Ϲ̶���һ���ʵ��ɣ�����һ����Ϊ�ʵ��С��С������m=0.2kg��ѹ�����ʵ�����A���ֹ�ͷţ�С��͵��ɲ��������С��պ�����DEN������£���
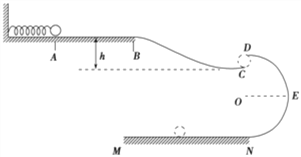
(1)С��պ���ͨ��D��ʱ�ٶȵĴ�С
(2)С��N��ʱ�ٶȵĴ�С���ܵ������֧�����Ĵ�С
(3)ѹ���ĵ��������еĵ�������
���𰸡���1��С��D��ʱ���ٶ�Ϊ2m/s��
��2��С��N��ʱ�ٶȵĴ�С��2![]() m/s���Թ����ѹ����12N��
m/s���Թ����ѹ����12N��
��3��ѹ���ĵ��������еĵ�������Ϊ0.44J��
�������������������1��С��պ�����DEN������£����ڰ�Բ��ߵ�D����У�
![]()
��![]()
��2����D�㵽N�㣬�ɻ�е���غ�ã� ![]() mvD2+mg2r=
mvD2+mg2r=![]() mvN2
mvN2
�������ݵã�vN=2![]() m/s��
m/s��
��N���� ![]()
�� N=6mg=12N
����ţ�ٵ�������֪��С��N��ʱ�Թ����ѹ����СΪ12N��
��3�������ƿ�С��Ĺ����У����ɶ�С�������Ĺ�W���ڵ��������еĵ�������Ep�����ݶ��ܶ�����
W-��mgL+mgh=![]() mvD2-0
mvD2-0
W=��mgL-mgh+![]() mvD2=0��44J
mvD2=0��44J
��ѹ���ĵ��������еĵ�������Ϊ0��44J