题目内容
在宇宙探索中,科学家发现某颗行星的质量和半径均为地球的1/2,宇航员登陆到该行星的表面时,将长度L=0.45m的细绳一端固定,另一端系质量m=0.1kg的金属球,并让金属球恰好能在竖直面内作圆周运动。已知地球表面重力加速度g=10m/s2。求:
⑴该行星表面的重力加速度g′;
⑵金属球通过最高点时线速度大小;
⑶金属球通过最低点时线速度大小
⑴该行星表面的重力加速度g′;
⑵金属球通过最高点时线速度大小;
⑶金属球通过最低点时线速度大小
⑴g′=20m/s2;⑵v1=3m/s;⑶v2=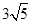 m/s。
m/s。
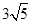 m/s。
m/s。试题分析:⑴设地球半径为M,半径为R,在地球表面有:
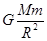 ≈mg ①
≈mg ①设行星半径为M′,半径为R′,在行星表面有:
 ≈mg′ ②
≈mg′ ②根据题意有:M=2M′,R=2R′, ③
由①②③式联立解得:g′=2g=20m/s2
⑵金属球通过最高点时,设其速度为v1,由于小球恰能经过最高点,因此此时只受重力mg′作用,根据牛顿第二定律有:mg′=
 ④
④由④式解得:v1=
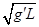 =
= m/s=3m/s
m/s=3m/s⑶设小球运动至最低时速度为v2,在整个运动过程中,小球只受mg′和细绳的拉力T作用,又因为拉力T的方向始终与小球速度方向垂直,因此整个运动过程中拉力T始终不做功,在小球由最高点运动至最低点的过程中,根据动能定理有:mg′×2L=
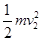 -
-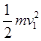 ⑤
⑤由④⑤式联立解得:v2=
 =
=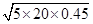 m/s=
m/s=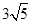 m/s
m/s
练习册系列答案
相关题目
 如图所示,在光滑水平地面上有一固定的挡板,挡板上固定一个轻弹簧。现有一质量
如图所示,在光滑水平地面上有一固定的挡板,挡板上固定一个轻弹簧。现有一质量 ,长
,长 的小车
的小车 (其中
(其中 为小车的中点,
为小车的中点, 部分粗糙,
部分粗糙, 部分光滑),一质量为
部分光滑),一质量为 的小物块(可视为质点),放在车的最左端,车和小物块一起以
的小物块(可视为质点),放在车的最左端,车和小物块一起以 的速度在水平面上向右匀速运动,车撞到挡板后瞬间速度变为零,但未与挡板粘连。已知车
的速度在水平面上向右匀速运动,车撞到挡板后瞬间速度变为零,但未与挡板粘连。已知车 0.3,重力加速度
0.3,重力加速度 。求:
。求:
 端多远。
端多远。
 的说法正确的是( )
的说法正确的是( )


