题目内容
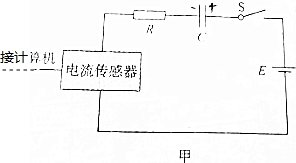
15. 用如图①所示的实验装置验证机械能守恒定律
用如图①所示的实验装置验证机械能守恒定律(1)下面列举了该实验的几个操作步骤:
A.用天平测量出重锤的质量;
B.松开悬挂纸带的夹子,同时接通电源开关打出一条纸带;
C.测量打出的纸带行某些点之间的距离;
D.根据测量的结果计算重锤下落过程中减少的重力势能是否等于增加的动能.其中操作错误的步骤是B,其正确步骤应该是先开电源再放纸带.
(2)某同学用正确的实验操作,得到如图②所示的纸带,测出点A、C间的距离为14.77,点C、E间的距离为 16.33cm.已知当地的重力加速度为9.8m/s2,重锤的质量为m=1.0kg,则重锤在下落过程中受到的平均阻力F1=0.05N.

(3)某同学上交的实验报告显示重锤的动能略大于重锤的势能,则下列原因中可能是BC
A.重锤的质量测量发生错误
B.该同学编造了实验数据
C.交流电源的频率不等于50Hz
D.重锤下落受到的阻力过大.
分析 根据实验原理与操作步骤一一分析:①验证:mgh与$\frac{1}{2}m{v}^{2}$的关系,m约掉了,不需要测量m;②先接通电源后释放纸带;③取点迹清晰的几个点,算出一个瞬时速度即可;④应让重物从靠近打点计时器处释放⑤不能根据h=$\frac{1}{2}$gt2求出物体运动重力加速度,而应该查找当地的重力加速度.
(2)根据连续相等时间内的位移之差是一恒量求出加速度的大小,通过牛顿第二定律求出阻力的大小
解答 解:(1)实验中若松开夹子的同时打开电源,则在打点计时器打点时,纸带已经下落了一段时间;不是从零开始的自由落体运动;故应先开电源,待稳定后再放纸带;
(2)由运动学公式可得:加速度$a=\frac{△x}{(2T)^{2}}$,
代入数据得:$a=\frac{△x}{{(2T)}^{2}}=\frac{16.33-14.77}{4×0.02×2}cm/{s}^{2}=975cm{/}^{2}=9.75$m/s2
根据牛顿第二定律得,mg-f=ma,
解得f=mg-ma=1×(9.8-9.75)N=0.05N.
(3)实验报告显示重锤增加的动能略大于重锤减少的重力势能,说明测量的物体的速度偏大或者是物体的重力势能偏小,
A、由重锤下落过程中mgh=$\frac{1}{2}$mv2可知,重锤的质量与实验的数据无关,所以重锤的质量测量错误不会影响实验的数据,故A错误;
B、该同学若自编了实验数据,可能导致重锤增加的动能略大于重锤减少的重力势能,故B正确;
C、交流电源的频率不等于50HZ.此时点之间的时间间隔不是0.02s,所以此时的测量的速度可能会大于真实的数值,导致重锤增加的动能略大于重锤减少的重力势能,故C正确;
D、重锤下落时受到的阻力过大,会使物体的速度减小,不会使物体的动能变大,故D错误;
故选:BC.
故答案为:(1)B;先开电源,再放纸带;(2)0.05N,(3)BC
点评 纸带问题的处理是力学实验中常见的问题.我们可以纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度,从而进一步根据物理规律得出实验结论.

 名校课堂系列答案
名校课堂系列答案| A. | 第一秒末的速度 | B. | 第二秒末速度 | ||
| C. | 最初一秒内的位移 | D. | 最后一秒内的位移 |
| A. | 点迹记录了物体运动的时间 | |
| B. | 点迹记录了物体在不同时刻的位置和某段时间内的位移 | |
| C. | 实验器材中必不可少的是秒表 | |
| D. | 实验器材中必不可少的是刻度尺 |
 在军事演习中,某空降兵从飞机上跳下,他的速度图象如图所示.下列关于该空降兵在0~t1和t1~t2时间内的平均速度$\overline{v}$的结论正确的是( )
在军事演习中,某空降兵从飞机上跳下,他的速度图象如图所示.下列关于该空降兵在0~t1和t1~t2时间内的平均速度$\overline{v}$的结论正确的是( )| A. | 0~t1内,$\overline{v}$=$\frac{{v}_{1}}{2}$ | B. | t1~t2内,$\overline{v}$>$\frac{{v}_{1}+{v}_{2}}{2}$ | ||
| C. | t1~t2内,$\overline{v}$=$\frac{{v}_{1}+{v}_{2}}{2}$ | D. | t1~t2内,$\overline{v}$<$\frac{{v}_{1}+{v}_{2}}{2}$ |


 如图所示是一质点从原点出发的v-t图象,根据图象求:
如图所示是一质点从原点出发的v-t图象,根据图象求:
 如图所示,细线穿在圆珠笔的杆中,一端拴住小物体,另一端用一只手握住,另一只手抓住圆珠笔杆并用力转动,使小物体做圆周运动.作用在小物体上的细线的拉力,近似地认为提供了圆周运动所需的向心力,而细线的拉力可用牵住细线的手的感觉来判断.
如图所示,细线穿在圆珠笔的杆中,一端拴住小物体,另一端用一只手握住,另一只手抓住圆珠笔杆并用力转动,使小物体做圆周运动.作用在小物体上的细线的拉力,近似地认为提供了圆周运动所需的向心力,而细线的拉力可用牵住细线的手的感觉来判断.