题目内容
9.宇航员站在一星球表面上的某处,以和水平方向成θ角的初速度V0斜向上抛出一个小球,不计大气阻力,小球的落点和抛出点在同一个水平面内,这两点之间的距离(射程)为L.已知该星球的半径为R,万有引力常数为G.求该星球的质量M.分析 先根据斜抛运动的分运动公式列式求解重力加速度;再根据重力等于万有引力列式求解该星球的质量M.
解答 解:对斜抛运动,竖直分速度为v0sinθ,水平分速度为v0cosθ,根据分运动公式,有:
x=L=(v0cosθ)t
y=0=(v0sinθ)t-$\frac{1}{2}g{t}^{2}$
联立解得:
g=$\frac{2{v}_{0}^{2}sinθcosθ}{L}$=$\frac{{v}_{0}^{2}sin2θ}{L}$
在星球表面,忽略星球自转,重力等于万有引力,故:
mg=G$\frac{Mm}{{R}^{2}}$
联立解得:
M=$\frac{{v}_{0}^{2}{R}^{2}}{GL}sin2θ$
答:该星球的质量M为$\frac{{v}_{0}^{2}{R}^{2}}{GL}sin2θ$.
点评 对斜抛运动,关键是通过运动的合成与分解的方法求解重力加速度;然后运用重力等于万有引力列式求解星球的质量;基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.南京青奥会上留下了许多精彩的瞬间.下列运动员比赛过程中可视为质点的是( )
| A. |  跳水 | B. |  鞍马 | C. |  马拉松 | D. |  吊环 |
4.火星和地球质量之比为P,火星和地球的半径之比为q,则火星表面处和地球表面处的重力加速度之比为( )
| A. | $\frac{p}{{q}^{2}}$ | B. | p•q2 | C. | $\frac{p}{q}$ | D. | p•q |
14. 2013年4月出现“火星合日”的天象,“火星合日”是指火星、太阳、地球三者之间形成一条直线时,从地球的方位观察,火星位于太阳的正后方,火星被太阳完全遮蔽的现象,如图所示;已知地球、火星绕太阳运行的方向相同,若把火星和地球绕太阳运行的轨道视为圆,火星绕太阳公转周期约等于地球公转周期的2倍,由此可知( )
2013年4月出现“火星合日”的天象,“火星合日”是指火星、太阳、地球三者之间形成一条直线时,从地球的方位观察,火星位于太阳的正后方,火星被太阳完全遮蔽的现象,如图所示;已知地球、火星绕太阳运行的方向相同,若把火星和地球绕太阳运行的轨道视为圆,火星绕太阳公转周期约等于地球公转周期的2倍,由此可知( )
 2013年4月出现“火星合日”的天象,“火星合日”是指火星、太阳、地球三者之间形成一条直线时,从地球的方位观察,火星位于太阳的正后方,火星被太阳完全遮蔽的现象,如图所示;已知地球、火星绕太阳运行的方向相同,若把火星和地球绕太阳运行的轨道视为圆,火星绕太阳公转周期约等于地球公转周期的2倍,由此可知( )
2013年4月出现“火星合日”的天象,“火星合日”是指火星、太阳、地球三者之间形成一条直线时,从地球的方位观察,火星位于太阳的正后方,火星被太阳完全遮蔽的现象,如图所示;已知地球、火星绕太阳运行的方向相同,若把火星和地球绕太阳运行的轨道视为圆,火星绕太阳公转周期约等于地球公转周期的2倍,由此可知( )| A. | “火星合日”约每1年出现一次 | |
| B. | “火星合日”约每4年出现一次 | |
| C. | 火星的公转半径约为地球公转半径的$\root{3}{4}$倍 | |
| D. | 火星的公转半径约为地球公转半径的8倍 |
1.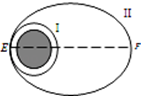 今年5月,信使号水星探测器陨落在水星表面.之前,工程师通过向后释放推进系统中的高压氦气来提升轨道,使其寿命再延长一个月,如图所示,释放氦气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氦气后探测器进入椭圆轨道Ⅱ,忽略探测器在椭圆轨道上所受阻力.则下列说法正确的是( )
今年5月,信使号水星探测器陨落在水星表面.之前,工程师通过向后释放推进系统中的高压氦气来提升轨道,使其寿命再延长一个月,如图所示,释放氦气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氦气后探测器进入椭圆轨道Ⅱ,忽略探测器在椭圆轨道上所受阻力.则下列说法正确的是( )
 今年5月,信使号水星探测器陨落在水星表面.之前,工程师通过向后释放推进系统中的高压氦气来提升轨道,使其寿命再延长一个月,如图所示,释放氦气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氦气后探测器进入椭圆轨道Ⅱ,忽略探测器在椭圆轨道上所受阻力.则下列说法正确的是( )
今年5月,信使号水星探测器陨落在水星表面.之前,工程师通过向后释放推进系统中的高压氦气来提升轨道,使其寿命再延长一个月,如图所示,释放氦气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氦气后探测器进入椭圆轨道Ⅱ,忽略探测器在椭圆轨道上所受阻力.则下列说法正确的是( )| A. | 探测器在轨道I的运行周期比在轨道Ⅱ的大 | |
| B. | 探测器在轨道Ⅱ上某点的速率可能等于在轨道Ⅰ上速率 | |
| C. | 探测器在轨道Ⅰ和轨道Ⅱ上的E处加速度相同 | |
| D. | 探测器在轨道Ⅱ上远离水星过程中,势能和动能均增大 |
18.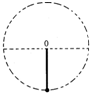 为了测量某行星的质量和半径,宇航员记录了登陆舱在该行星表面做圆周运动的周期T,登陆舱在行星表面着陆后,用弹簧称称量一个质量为m的砝码读数为N.已知引力常量为G.则下列计算中正确的是( )
为了测量某行星的质量和半径,宇航员记录了登陆舱在该行星表面做圆周运动的周期T,登陆舱在行星表面着陆后,用弹簧称称量一个质量为m的砝码读数为N.已知引力常量为G.则下列计算中正确的是( )
 为了测量某行星的质量和半径,宇航员记录了登陆舱在该行星表面做圆周运动的周期T,登陆舱在行星表面着陆后,用弹簧称称量一个质量为m的砝码读数为N.已知引力常量为G.则下列计算中正确的是( )
为了测量某行星的质量和半径,宇航员记录了登陆舱在该行星表面做圆周运动的周期T,登陆舱在行星表面着陆后,用弹簧称称量一个质量为m的砝码读数为N.已知引力常量为G.则下列计算中正确的是( )| A. | 在该行星的第一宇宙速度为$\frac{NT}{2πm}$ | B. | 该行星的密度为$\frac{3G}{{π{T^2}}}$ | ||
| C. | 该行星的质量为$\frac{{N}^{3}{T}^{4}}{16{π}^{4}{m}^{3}}$ | D. | 该行星的半径为$\frac{4{π}^{2}N{T}^{2}}{m}$ |
19.一物体静止在斜面上,下面说法正确的是( )
| A. | 物体受到重力,斜面的支持力,下滑力和静摩擦力作用 | |
| B. | 物体对斜面的压力就是重力在垂直于斜面方向的分力 | |
| C. | 当增加斜面倾角时,只要物体不滑动,它受的摩擦力随斜面倾角的增大而减小 | |
| D. | 当增加斜面倾角时,一旦物体沿斜面下滑,它所受的摩擦力将随斜面倾角的增大而减小 |
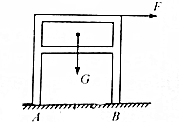 如图所示,桌子在水平力F的作用下匀速缓慢移动,已知桌子重G=100N,桌腿与地面的摩擦系数μ=0.2,桌子的宽、高相等.求:
如图所示,桌子在水平力F的作用下匀速缓慢移动,已知桌子重G=100N,桌腿与地面的摩擦系数μ=0.2,桌子的宽、高相等.求: