题目内容

若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球，测出小球的水平射程为L．已知月球半径为R，万有引力常量为G．则下列说法正确的是（　　）
分析：宇航员在月球上自高h处以初速度v0水平抛出一物体，测出物体的水平射程为L，根据水平射程和初速度求出运动的时间，根据h=
1
2
gt2求出月球表面的重力加速度大小；由g=
Gm
r2
求得月球的质量；根据重力提供向心力求出卫星的第一宇宙速度；由质量与半径可求得平均密度．
解答：解：A、平抛运动的时间t=
L
v0
．再根据h=
1
2
gt2得，得g月=
2h
v
2
0
L2
，故A正确
    B、由g月=
Gm月
R2
与g月=
2h
v
2
0
L2
，可得：m月=
2hR2
v
2
0
GL2
．故B错误．
    C、第一宇宙速度：v=
g月R
=
2h
v
2
0
L2
R
=v=
v0
L
2hR
，故C正确
   D、月球的平均密度ρ=
m月
4
3
πR3
=
3h
v
2
0
2πGR2L2
，故D错误
故选：AC
点评：解决本题的关键知道平抛运动在水平方向上和竖直方向上的运动规律，以及掌握万有引力提供向心力以及万有引力等于重力这两个理论的运用
练习册系列答案
相关题目
图示是我国的“探月工程”向月球发射一颗绕月探测卫星“嫦娥一号”过程简图．月球探测计划“嫦娥工程”预计在2017年送机器人上月球，实地采样送回地球，为载人登月及月球基地选址做准备．设想我国宇航员随“嫦娥”号登月飞船绕月球飞行，飞船上备有以下实验仪器：
A．计时表一只，B．弹簧秤一把，C．已知质量为m的物体一个，D．天平一只（附砝码一盒）．
在飞船贴近月球表面时可近似看成绕月球做匀速圆周运动，宇航员测量出飞船在靠近月球表面的圆形轨道绕行N圈所用的时间为t．飞船的登月舱在月球上着陆后，遥控机器人利用所携带的仪器又进行了第二次测量，利用上述两次测量的物理量可出推导出月球的半径和质量．（已知万有引力常量为G），要求：
（1）说明机器人是如何进行第二次测量的？
（2）试推导用上述测量的物理量表示的月球半径和质量的表达式．
（3）若已知R月=
1
4
R地，g月=
1
6
g地，则近月卫星的运行速度约为近地卫星运行速度的多少倍？
中国首个月球探测计划“嫦娥工程”将分三个阶段实施：首先在2007年发射环绕月球的卫星“嫦娥一号”，深入了解月球；到2012年发射月球探测器，在月球上进行实地探测；到2017年送机器人上月球，建立观测站，实地实验采样并返回地球，为载人登月及月球基地选址做准备．设想我国宇航员随“嫦娥”号登月飞船登陆月球，在飞船贴近月球表面时可近似看成绕月球做匀速圆周运动，飞船上备有以下实验仪器：A．计时表一只，B．弹簧秤一把，C．已知质量为m的物体一个，D．天平一只（附砝码一盒）．宇航员测量出飞船在靠近月球表面的圆形轨道绕行N圈所用的时间为t．飞船在月球上着陆后，宇航员利用所带的仪器又进行了第二次测量，并利用测量结果计算出了月球的半径和质量．若已知万有引力常量为G，则：
（1）说明宇航员是如何进行第二次测量的？
（2）利用宇航员测量的量（用符号表示）来求月球的半径和质量．
中国首个月球探测计划“嫦娥工程”预计在2017年送机器人上月球，实地采样送回地球，为载人登月及月球基地选址做准备．设想我国宇航员随“嫦娥”号登月飞船绕月球飞行，飞船上备有以下实验仪器：A．计时表一只，B．弹簧秤一把，C．已知质量为m的物体一个，D．天平一只（附砝码一盒）．在飞船贴近月球表面时可近似看成绕月球做匀速圆周运动，宇航员测量出飞船在靠近月球表面的圆形轨道绕行N圈所用的时间为t．飞船的登月舱在月球上着陆后，遥控机器人利用所携带的仪器又进行了第二次测量，科学家利用上述两次测量数据便可计算出月球的半径和质量．若已知万有引力常量为G，则：
（1）简述机器人是如何通过第二次测量物体在月球所受的重力F
（2）试利用测量数据（用符号表示）求月球的半径和质量．

寻找地外文明与地球外的生存环境一直是科学家们不断努力的目标。如图所示是我国的“探月工程”向月球发射一颗绕月探测卫星“嫦娥一号”过程简图．月球探测计划“嫦娥工程”预计在2017年送机器人上月球，实地采样送回地球，为载人登月及月球基地选址做准备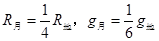．现设想你是宇航员随“嫦娥”号登月飞船绕月球飞行，飞船上备有以下实验仪器：A．计时表一只，B．弹簧秤一把，C．已知质量为m的物体一个，D．天平一台(附砝码一盒)．在飞船贴近月球表面时可近似看成绕月球做匀速圆周运动，你已测量出飞船在靠近月球表面的圆形轨道绕行N圈所用的时间为T．为了能测算出月球的半径和质量，飞船的登月舱在月球上着陆后，你遥控机器人利用所携带的仪器又进行了第二次测量．（已知万有引力常量为G），求：

（1）说明你给机器人发的指令,如何让它进行第二次测量的？

（2）试推导用上述测量的物理量表示的月球半径和质量的表达式．

 (3)若已知，则可以推知近月卫星的运行速度约为近地卫星运行速度的多少倍？

 

中国首个月球探测计划“嫦娥工程”预计在2017年送机器人上月球，实地采样送回地球，为载人登月及月球基地选址做准备。设想我国宇航员随“嫦娥”号登月飞船绕月球飞行，飞船上备有以下实验仪器：A.计时表一只，B.弹簧秤一把，C.已知质量为m的物体一个，D.天平一只（附砝码一盒）。在飞船贴近月球表面时可近似看成绕月做匀速圆周运动，宇航员测量出飞船在靠近月球表面的圆形轨道绕行N圈所用时间为t，飞船的登月舱在月球上着陆后，遥控机器人利用所携带的仪器又进行第二次测量，科学家利用上述两次测量数据便可计算出月球的半径和质量。若已知万有引力常量为G，则：

（1）遥控机器人在第二次测量中利用所携带的什么仪器完成物体在月球所受重力F的测量。

（2）试利用测量数据（用符号表示）球月球的半径和质量。

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网