题目内容
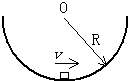如图，一质量为m的物体（可视为质点），沿半径为R的圆形轨道滑行，如图所示，经过最低点的速度为v，物体与轨道之间的动摩擦因数为μ，则它在最低点对轨道的压力为m（g+
）
| v2 |
| R |
m（g+
）
，受到轨道的摩擦力为| v2 |
| R |
μm（g+
）
| v2 |
| R |
μm（g+
）
．| v2 |
| R |
分析：物块滑到轨道最低点时，由重力和轨道的支持力提供物块的向心力，由牛顿第二定律求出支持力，再由摩擦力公式求解摩擦力．
解答：解：物块滑到轨道最低点时，由重力和轨道的支持力提供物块的向心力，由牛顿第二定律得
FN-mg=m
得到FN=m（g+
）
则当小物块滑到最低点时受到的摩擦力为f=μFN=μm（g+
）
故答案为：m（g+
）；μm（g+
）
FN-mg=m
| v2 |
| R |
得到FN=m（g+
| v2 |
| R |
则当小物块滑到最低点时受到的摩擦力为f=μFN=μm（g+
| v2 |
| R |
故答案为：m（g+
| v2 |
| R |
| v2 |
| R |
点评：本题是牛顿定律和向心力、摩擦力知识的简单综合应用，关键是分析向心力的来源．
练习册系列答案
相关题目
如图，一质量为M的物块被两竖直板用力F夹住，物与板间的摩擦系数为μ，要使物块匀速向上运动而两竖直板不动，向上拉物块的力最小为
如图，一质量为M的物块静止在桌面边缘，桌面离水平地面高度为h，质量为m的子弹以水平速度v0射入物块后，以水平速度
如图：一质量为M的物块被两竖直板用力F夹住，物与板间的摩擦系数为μ，要使物块匀速向上运动而两竖直板不动，向上拉物块的力为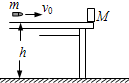
如图，一质量为M的物块静止在桌面边缘，桌面离水平地面的高度为h．一质量为m的子弹以水平速度v0射入物块后，以水平速度v0/2 射出．重力加速度为g．求：