题目内容
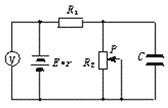
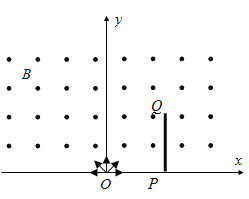
【题目】如图所示,在x轴上方(含x轴)存在垂直xOy平面向外的匀强磁场,在x轴上距离原点x0处垂直于x轴放置一个长度也为x0、厚度不计的薄板PQ,粒子打在板上即被吸收。坐标原点O处有一粒子源,可垂直于磁场向磁场内各个方向均匀发射速率相同的同种粒子,粒子速度大小为v、质量为m、带电量为+q。现观察到沿y轴正方向射入磁场的粒子垂直打在薄板的上端Q,不计带电粒子的重力和粒子间的相互作用力,不考虑薄板吸收粒子后产生的电场,则下列说法正确的有( )
A.磁场的磁感应强度大小为![]()
B.打在薄板左侧的粒子数占发射总粒子数的![]()
C.打在薄板右侧的粒子数占发射总粒子数的![]()
D.打在薄板上的粒子在磁场中运动的最长时间与最短时间的比值为3∶1
【答案】AC
【解析】
A.由题意,“沿y轴正方向射入磁场的粒子垂直打在薄板的上端Q”,可得粒子运动的半径:
R=x0
由洛伦兹力提供向心力,得:
![]()
解得:
![]()
A正确;
BC.沿y轴正方向射出的粒子恰能达到挡板的最上端;由图1可知与x轴正方向夹角为30°的粒子能达到挡板左侧最低点,则能打到挡板左侧的粒子的速度范围为60°范围;同理与x轴正方向夹角为150°的粒子能达到挡板右侧最低点(如图2所示),沿x轴负方向射出的粒子能达到挡板的最高点,则能打到挡板右侧的粒子的速度范围为30°范围;则打在薄板右侧的粒子数占发射总粒子数的![]() ,B错误,C正确;
,B错误,C正确;
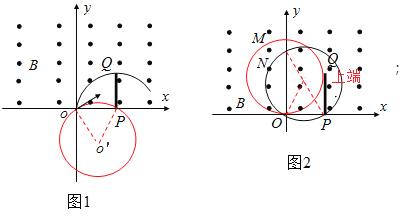
D.与x轴正方向夹角为30°的粒子能达到挡板左侧最低点的粒子运动时间最短,此粒子在磁场中转过的角度为60°;与x轴正方向夹角为150°的粒子达到挡板右侧最低点的粒子运动时间最长,此粒子在磁场中转过的角度为300°,根据
![]()
可知打在薄板上的粒子在磁场中运动的最长时间与最短时间的比值为300°:60°=5∶1,D错误。
故选AC。

【题目】为探究一定质量的气体在温度不变时,压强与体积的关系,设计了如下实验:
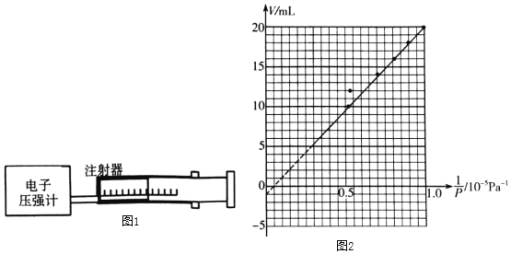
(1)用注射器封闭一部分气体并连接装置,如图1所示,用注射器读出封闭气体的体积V,由电子压强计读出压强P,改变气体体积得出了一组据如表
次数 | 1 | 2 | 3 | 4 | 5 | 6 |
体积V/mL | 20 | 18 | 16 | 14 | 12 | 10 |
压强P/105Pa | 1.000 | 1.105 | 1.235 | 1.400 | 1.815 | 1.909 |
压强的倒数 | 1.000 | 0.9.5 | 0.810 | 0.714 | 0.551 | 0.524 |
(2)由上表数据在坐标纸上画出V﹣![]() 图象,如图2所示。由图象可以看出第_____组数据误差最大,原因可能是实验过程中_____。
图象,如图2所示。由图象可以看出第_____组数据误差最大,原因可能是实验过程中_____。
A.封闭气体有部分漏出
B.用手握住注射器进行实验
C.缓慢推动注射器活塞
(3)若该实验的差仅由注射器与传感器之间细管中的气体体积V0导致的。由上面图象得V0大小为_____mL(结果保留1位有效数字);为减少该实验误差,开始封闭气体体积应尽量_____(填“大”或者“小“)一些。