Question

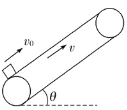
【题目】如图所示，倾角为 θ＝37°的传送带以速度 v＝2 m/s 沿图示方向匀速运动。现将一 质量为 2 kg 的小木块，从传送带的底端以 v0＝4 m/s 的初速度，沿传送带运动方 向滑上传送带。已知小木块与传送带间的动摩擦因数为 μ＝0.5，传送带足够长， sin 37°＝0.6，cos 37°＝0.8，取 g＝10 m/s2。小物块从滑上传送带至到达最高点的过程中，下列说法正确的是（ ）

A.运动时间为 0.4 s

B.发生的位移为 1.2 m

C.产生的热量为 9.6 J

D.摩擦力对小木块所做功为 12.8 J

Answer 1

【答案】C

【解析】

考查牛顿第二定律的应用，传送带模型。

A．初始时，，小木块相对于传送带向上运动，摩擦力向下，有：

解得，沿斜面向下，减速到2m/s，用时：

之后摩擦力向上，最大静摩擦力：

小木块继续减速向上运动，直到最高点时速度为零：

解得，沿斜面向下，用时：

所以小物块从滑上传送带至到达最高点的过程中，一共用时：

A错误；

B．4m/s减速到2m/s过程中：

解得，

2m/s减速到0过程中：

解得，则总位移：

B错误；

C．4m/s减速到2m/s 过程中，相对路程：

2m/s减速到0过程中，相对路程：

总相对路程：

产生的热量为：

C正确；

D．由动能定理：

解得，D错误。

故选C。