题目内容
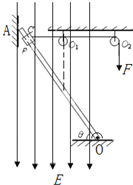
如图所示，一绝缘轻绳绕过无摩擦的两轻质小定滑轮O1、O2，一端与质量m=0.2kg的带正电小环P连接，且小环套在绝缘的均匀光滑直杆上（环的直径略大于杆的截面直径），已知小环P带电q=4×10-5C，另一端加一恒定的力F=4N。已知直杆下端有一固定转动轴O，上端靠在光滑竖直墙上的A处，其质量M=1kg，长度L=1m，杆与水平面的夹角为θ=530，直杆上C点与定滑轮在同一高度，杆上CO=0.8m，滑轮O1在杆中点的正上方，整个装置在同一竖直平面内，处于竖直向下的大小E=5×104N/C的匀强电场中。现将小环P从C点由静止释放，求：（取g＝10m／s2）
（1）刚释放小环时，竖直墙A处对杆的弹力大小；
（2）下滑过程中小环能达到的最大速度；
（3）若仅把电场方向反向，其他条件都不变，则环运动过程中电势能变化的最大值。
（1）N=2.95（2）
（3）
【解析】
试题分析：（1）设环受到重力为Gp，电场力为F，绳子拉力为 T，对环受力分析得：T cos370+N1=(Gp+F) cos530 代入数据得：N1=0.8N （2分）
竖直墙A处对杆的弹力为N，对杆分析得：
代入数据得：N=2.95(N)……（3分）
（2）设小环下滑时，绳与杆之间的夹角为α时，小环速度最大，此时小环沿杆方向的合外力为零（F+G）sin530=Fsinα得：α=370 ……（2分）
也即小环滑至O1正下方时，小环速度最大，此时小环下滑s=0.3m
……（2分）
（3）当电场力反向，电场力正好与重力平衡，当小环下滑至绳拉力方向与杆垂直时，速度最大。由对称性得：小环下滑s1=2scos530
cos530=2×0.3×0.6×0.6(m)=0.216(m),此时电势能变化值最大
（4分）
考点：考查了力学综合
点评：关键是对物体受力分析，结合共点力平衡条件，列式求解
（2013?奉贤区二模）如图所示，一绝缘轻绳绕过无摩擦的两轻质小定滑轮O1、O2，一端与质量m=0.2kg的带正电小环P连接，且小环套在绝缘的均匀光滑直杆上（环的直径略大于杆的截面直径），已知小环P带电q=4×10-5C，另一端加一恒定的力F=4N．已知直杆下端有一固定转动轴O，上端靠在光滑竖直墙上的A处，其质量M=1kg，长度L=1m，杆与水平面的夹角为θ=530，直杆上C点与定滑轮在同一高度，杆上CO=0.8m，滑轮O1在杆中点的正上方，整个装置在同一竖直平面内，处于竖直向下的大小E=5×104N/C的匀强电场中．现将小环P从C点由静止释放，求：（取g=10m/s2）
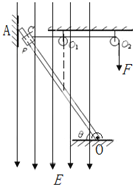如图所示，一绝缘轻绳绕过无摩擦的两轻质小定滑轮O1、O2，一端与质量m=0.2kg的带正电小环P连接，且小环套在绝缘的均匀光滑直杆上（环的直径略大于杆的截面直径），已知小环P带电q=4×10-5C，另一端加一恒定的力F=4N．已知直杆下端有一固定转动轴O，上端靠在光滑竖直墙上的A处，其质量M=1kg，长度L=1m，杆与水平面的夹角为θ=530，直杆上C点与定滑轮在同一高度，杆上CO=0.8m，滑轮O1在杆中点的正上方，整个装置在同一竖直平面内，处于竖直向下的大小E=5×104N/C的匀强电场中．现将小环P从C点由静止释放，求：（取g=10m/s2）