题目内容
9. 如图所示的弹簧振子,其固有周期为T,把振子从平衡位置O拉到B点后由静止释放,OB距离为振幅A.弹簧振子振动过程中,如以通过B点的时刻作为计时的开始时刻,问:
如图所示的弹簧振子,其固有周期为T,把振子从平衡位置O拉到B点后由静止释放,OB距离为振幅A.弹簧振子振动过程中,如以通过B点的时刻作为计时的开始时刻,问:(1)若规定向右为正方向,在一个周期内,哪段时间位移为正,哪段时间位移为负?
(2)在t=$\frac{T}{4}$时,振子的位移和速度怎样?
(3)在t=$\frac{T}{2}$时,振子的位移和速度怎样?
(4)振子完成一次全振动的路程是多少?
分析 (1)弹簧振子的位移为离开离开平衡位置的位移,不是以出发点为0.由此结合弹簧振子运动的周期性即可正确解答;
(2)在t=$\frac{T}{4}$时,先判断出振子的位置,然后结合振动的特点解答振子的位移和速度;
(3)在t=$\frac{T}{2}$时,先判断出振子的位置,然后结合振动的特点解答振子的位移和速度;
(4)振子完成一次全振动的路程为4倍的振幅,由此解答即可.
解答 解:(1)若规定向右为正方向,在一个周期内,前$\frac{T}{4}$周期内由B向O点运动,位移为正;第2个$\frac{T}{4}$周期内由O点向A点运动,位移为负;第3个$\frac{T}{4}$内,振子由A点向O点运动,位移为负;第4个$\frac{T}{4}$内振子由O向B运动,位移为正;
(2)由(1)的分析可知,在t=$\frac{T}{4}$时振子经过平衡位置O点,振子的位移为零,逐渐减小;振子向左运动,速度最大;
(3)在t=$\frac{T}{2}$时振子到达A点,振子的位移为负的最大,速度为0;
(4)振子完成一次全振动的路程是4倍振幅,即4A.
答:(1)在一个周期内,0-$\frac{T}{4}$和$\frac{3}{4}T$-T时间内的位移为正,$\frac{T}{4}$-$\frac{3}{4}T$时间内的位移为负;
(2)在t=$\frac{T}{4}$时振子经过平衡位置O点,振子的位移为零,逐渐减小;振子向左运动,速度最大;
(3)在t=$\frac{T}{2}$时振子到达A点,振子的位移为负的最大,速度为0;
(4)振子完成一次全振动的路程是4倍振幅,即4A.
点评 本题关键根据简谐运动的位移时间图象得到弹簧振子的周期和振幅,然后结合结合位移的变化,分析质点的速度方向.

| A. | 若粒子的带电量和初动能相同,则离开电场时它们的偏向角φ相同 | |
| B. | 若质量不同的带电粒子由静止开始经相同电场加速后进入该偏转电场,则离开电场时它们的偏向角φ相同 | |
| C. | 若带电粒子由静止开始经相同电场加速后进入该偏转电场,离开电场时其偏移量y与粒子电荷量成正比 | |
| D. | 若带电粒子以相同的初速度进入该偏转电场,离开电场时其偏移量y与粒子的荷质比成正比 |
 如图所示,某极限运动爱好者(可视为质点)尝试一种特殊的高空运动.他身系一定长度的弹性轻绳,从距水面高度大于弹性轻绳原长的P点以水平初速度v0跳出.他运动到图中a点时弹性轻绳刚好拉直,此时速度与竖直方向的夹角为θ,轻绳与竖直方向的夹角为β,b为运动过程的最低点(图中未画出),在他运动的整个过程中未触及水面,不计空气阻力,重力加速度为g.下列说法正确的是( )
如图所示,某极限运动爱好者(可视为质点)尝试一种特殊的高空运动.他身系一定长度的弹性轻绳,从距水面高度大于弹性轻绳原长的P点以水平初速度v0跳出.他运动到图中a点时弹性轻绳刚好拉直,此时速度与竖直方向的夹角为θ,轻绳与竖直方向的夹角为β,b为运动过程的最低点(图中未画出),在他运动的整个过程中未触及水面,不计空气阻力,重力加速度为g.下列说法正确的是( )| A. | 极限运动爱好者从P点到b点的运动过程中机械能守恒 | |
| B. | .极限运动爱好者从P点到a点时间的表达式可能为$\frac{{v}_{0}}{gtanθ}$ | |
| C. | .极限运动爰好者到达a点时,tanθ=tanβ | |
| D. | .弹性轻绳原长的表达式可能为:$\frac{{v}_{0}^{2}}{gsinβtanθ}$ |
| A. | 火箭尾部向外喷气,喷出的气体反过来对火箭产生一个反作用力,从而让火箭获得了向前的推力 | |
| B. | 火箭尾部喷出的气体对空气产生一个作用力,空气的反作用力使火箭获得飞行的动力 | |
| C. | 卫星进入预定轨道之后,与地球之间不存在相互作用 | |
| D. | 火箭飞出大气层后,由于没有了空气,火箭虽然向后喷气,但也无法获得前进的动力 |
 甲、乙物体做直线运动,两物体的v-t图象如图所示,若它们的初速度的大小都为v0,末速度的大小都为v1,则在时间t1内甲物体的平均速度$\overline{{v}_{甲}}$=$\frac{{v}_{0}+{v}_{t}}{2}$,且$\overline{{v}_{甲}}$<$\overline{{v}_{乙}}$(选填“>”、“=”或“<”)
甲、乙物体做直线运动,两物体的v-t图象如图所示,若它们的初速度的大小都为v0,末速度的大小都为v1,则在时间t1内甲物体的平均速度$\overline{{v}_{甲}}$=$\frac{{v}_{0}+{v}_{t}}{2}$,且$\overline{{v}_{甲}}$<$\overline{{v}_{乙}}$(选填“>”、“=”或“<”) 质量为M1、半径为R的$\frac{1}{4}$光滑圆槽,与一个质量为M2的光滑弧形槽,相对地放在光滑水平面上,连接处与水平面相切.一个质量为m的物体从M1顶端正上方高为h0处自由落下,先沿M1槽下滑,后又滑到M2顶端时恰好与M2相对静止.
质量为M1、半径为R的$\frac{1}{4}$光滑圆槽,与一个质量为M2的光滑弧形槽,相对地放在光滑水平面上,连接处与水平面相切.一个质量为m的物体从M1顶端正上方高为h0处自由落下,先沿M1槽下滑,后又滑到M2顶端时恰好与M2相对静止. 某同学想在家里做用《单摆测定重力加速度》的实验,但没有合适的摆球,他找到了一块大小为3cm左右,外形不规则的大理石块代替小球.他设计的实验步骤是:
某同学想在家里做用《单摆测定重力加速度》的实验,但没有合适的摆球,他找到了一块大小为3cm左右,外形不规则的大理石块代替小球.他设计的实验步骤是: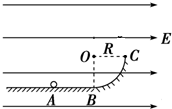 ABC表示竖直放在电场强度为E=104V/m的水平匀强电场中的绝缘光滑轨道,其中轨道的BC部分是半径为R的$\frac{1}{4}$圆环,轨道的水平部分与半圆环相切.A为水平轨道上的一点,而且AB=R=0.2m,把一质量m=0.1kg,带电量为q=+10-4C的小球,放在A点由静止释放后,求:(g=10m/s2)
ABC表示竖直放在电场强度为E=104V/m的水平匀强电场中的绝缘光滑轨道,其中轨道的BC部分是半径为R的$\frac{1}{4}$圆环,轨道的水平部分与半圆环相切.A为水平轨道上的一点,而且AB=R=0.2m,把一质量m=0.1kg,带电量为q=+10-4C的小球,放在A点由静止释放后,求:(g=10m/s2)