题目内容
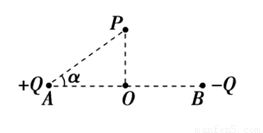
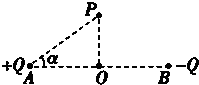 如图所示,相距为2d的A和B两点上固定着等量异种的两个点电荷,电荷量分别为+Q和-Q.在AB连线的中垂线上取一点P,垂足为O,∠PAO=α,求:
如图所示,相距为2d的A和B两点上固定着等量异种的两个点电荷,电荷量分别为+Q和-Q.在AB连线的中垂线上取一点P,垂足为O,∠PAO=α,求:(1)-Q在P点的场强的大小和方向;
(2)P点的场强的大小和方向;
(3)α为何值时,P点的场强最大,其最大值是多少?
分析:(1)根据点电荷的电场强度公式,结合几何关系,即可求解;
(2)根据矢量法则,结合三角函数,即可求解;
(3)根据表达式,即可求解.
(2)根据矢量法则,结合三角函数,即可求解;
(3)根据表达式,即可求解.
解答:解:(1)负电荷在P点产生电场强度大小为:E=
,
且r=
;
解得:E=
=
cos2α;
方向由P→B;
(2)如图所示,P点电场强度是正负电荷在P点产生电场强度的矢量和,
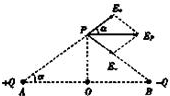
由图可知,EP=2Ecosα=
cosα=
cos3α;
方向向右.
(3)由上式表明,当α=0时,得:EPMAX=
,方向向右.
答:(1)-Q在P点的场强的大小
cos2α和方向P→B;(2)P点的场强的大小
cos3α和方向向右;(3)α为0时,P点的场强最大,其最大值是
.
| kQ |
| r2 |
且r=
| d |
| cosα |
解得:E=
| kQ | ||
(
|
| kQ |
| d2 |
方向由P→B;
(2)如图所示,P点电场强度是正负电荷在P点产生电场强度的矢量和,

由图可知,EP=2Ecosα=
| 2kQ | ||
(
|
| 2kQ |
| d2 |
方向向右.
(3)由上式表明,当α=0时,得:EPMAX=
| 2kQ |
| d2 |
答:(1)-Q在P点的场强的大小
| kQ |
| d2 |
| 2kQ |
| d2 |
| 2kQ |
| d2 |
点评:考查点电荷电场强度公式的应用,并掌握矢量性法则,注意几何关系与三角函数的运用.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
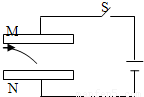
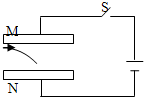 如图所示,相距为d的两块平行金属板M、N与电源相连,电键S闭合后,MN间有匀强电场,一个带电粒子,垂直于电场方向从M板边缘射入电场,恰好打在N板中央.若不计重力,下列说法正确的是( )
如图所示,相距为d的两块平行金属板M、N与电源相连,电键S闭合后,MN间有匀强电场,一个带电粒子,垂直于电场方向从M板边缘射入电场,恰好打在N板中央.若不计重力,下列说法正确的是( )