题目内容
12. 把一个小球用细绳悬挂起来,就成为一个摆.如图所示,已知摆长为L,最大偏角为θ,不计空气阻力,小球可视为质点.求:
把一个小球用细绳悬挂起来,就成为一个摆.如图所示,已知摆长为L,最大偏角为θ,不计空气阻力,小球可视为质点.求:(1)小球运动到O点时的速度是多大?
(2)小球经过最低点时绳子对小球的拉力大小?
分析 小球在摆动的过程中,只有重力做功,机械能守恒,根据机械能守恒定律求出小球运动到最低位置时的速度大小.在最低点,小球靠重力和拉力的合力提供向心力,根据牛顿第二定律求出细线的拉力大小.
解答 解:(1)由最大偏角θ处下落,到最低点时,竖直的高度差是:h=L(1-cosθ)
有机械能守恒定律知:
mgL(1-cosθ)=$\frac{1}{2}$mv2
得:v=$\sqrt{2gL(1-cosθ)}$
(2)在最低点合外力提供向心力:
F-mg=m$\frac{{v}^{2}}{L}$
解得:
F=3mg-2mgcosθ
答:(1)小球运动到最低位置时的速度是 $\sqrt{2gL(1-cosθ)}$.
(2)在最低点,细线的拉力为3mg-2mgcosθ.
点评 本题综合考查了机械能守恒定律和牛顿第二定律,难度不大,需加强这方面的训练,基础题.

练习册系列答案
相关题目
20.把一个质量为1kg的小球从5.0m高的桌面水平抛出,落到地面的位置与桌面边缘的水平距离为10m,则小球落地时的速度大小是(g=10m/s2)( )
| A. | 5m/s | B. | 10 m/s | C. | 14.1 m/s | D. | 15m/s |
17.下列说法中正确的是( )
| A. | 同种介质中,光的波长越短,传播速度越快 | |
| B. | 某同学在测单摆的周期时将全振动的次数多记了一次,则测出的周期偏小 | |
| C. | 泊松亮斑有力地支持了光的微粒说,杨氏干涉实验有力地支持了光的波动说 | |
| D. | 静止在地面上的人观察一条沿自身长度方向高速运动的杆,观察到的长度比杆静止时的长 |
4. 一台小型发电机产生的电动势随时间变化的规律为e=220$\sqrt{2}$sin100πtV.已知发电机线圈内阻为5.0Ω,外接一个电阻为95.0Ω 的灯泡,如图所示,则( )
一台小型发电机产生的电动势随时间变化的规律为e=220$\sqrt{2}$sin100πtV.已知发电机线圈内阻为5.0Ω,外接一个电阻为95.0Ω 的灯泡,如图所示,则( )
 一台小型发电机产生的电动势随时间变化的规律为e=220$\sqrt{2}$sin100πtV.已知发电机线圈内阻为5.0Ω,外接一个电阻为95.0Ω 的灯泡,如图所示,则( )
一台小型发电机产生的电动势随时间变化的规律为e=220$\sqrt{2}$sin100πtV.已知发电机线圈内阻为5.0Ω,外接一个电阻为95.0Ω 的灯泡,如图所示,则( )| A. | 交流电压表的示数为220$\sqrt{2}$V | |
| B. | 该交流电压的频率为100Hz | |
| C. | 线框在如图位置时,穿过线框的磁通量最大 | |
| D. | 发电机线圈内阻每秒钟产生的焦耳热为24.2J |
1.质点沿两个半径均为R的半圆弧由A运动到C,如图所示,则其路程和位移分别是( )

| A. | 0;0 | B. | 4R、方向向东;2πR、方向向东 | ||
| C. | 2πR;4R、方向向东 | D. | 2πR;4R |
2.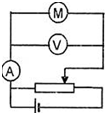 实际生活中,我们常常要选用参数恰当的元件,某同学用如图所示的电路进行小电机M的输出功率的研究(图中电表均为理想仪表),其实验步骤如下所述:连接好电路后,调节滑动变阻器,电动机未转动时,电压表的读数为U1,电流表的读数为I1;再调节滑动变阻器,电动机转动后电压表的读数为U2,电流表的读数为I2,则此时电动机的输出功率( )
实际生活中,我们常常要选用参数恰当的元件,某同学用如图所示的电路进行小电机M的输出功率的研究(图中电表均为理想仪表),其实验步骤如下所述:连接好电路后,调节滑动变阻器,电动机未转动时,电压表的读数为U1,电流表的读数为I1;再调节滑动变阻器,电动机转动后电压表的读数为U2,电流表的读数为I2,则此时电动机的输出功率( )
 实际生活中,我们常常要选用参数恰当的元件,某同学用如图所示的电路进行小电机M的输出功率的研究(图中电表均为理想仪表),其实验步骤如下所述:连接好电路后,调节滑动变阻器,电动机未转动时,电压表的读数为U1,电流表的读数为I1;再调节滑动变阻器,电动机转动后电压表的读数为U2,电流表的读数为I2,则此时电动机的输出功率( )
实际生活中,我们常常要选用参数恰当的元件,某同学用如图所示的电路进行小电机M的输出功率的研究(图中电表均为理想仪表),其实验步骤如下所述:连接好电路后,调节滑动变阻器,电动机未转动时,电压表的读数为U1,电流表的读数为I1;再调节滑动变阻器,电动机转动后电压表的读数为U2,电流表的读数为I2,则此时电动机的输出功率( )| A. | U2I2-U1I1 | B. | U2I2-I22$\frac{U_1}{I_1}$ | C. | U2I2+I22$\frac{U_1}{I_1}$ | D. | I22$\frac{U_1}{I_1}$ |
 一列横波波形如图所示.这列波振幅为4cm;波长为8m.经过2秒A质点第一次回到平衡位置,则这列波的周期为8s;频率为0.125Hz;波速为1m/s.若x=4m的质点此时正向下运动,则波的传播方向为左.
一列横波波形如图所示.这列波振幅为4cm;波长为8m.经过2秒A质点第一次回到平衡位置,则这列波的周期为8s;频率为0.125Hz;波速为1m/s.若x=4m的质点此时正向下运动,则波的传播方向为左. 如图所示,在光滑水平面上有质量均为m的A、B两物体,在水平面的右端有一轻弹簧,弹簧的右端固定在水平面右端的墙壁上,且A、B与弹簧在同一条水平线上,现给A向右的初速度v0使其向B运动并与B碰撞,碰后A、B粘在一起向弹簧运动,设在整个A、B与弹簧作用的过程中,弹簧都在弹性限度内,求弹簧在相互作用过程中的最大弹性势能Epm.
如图所示,在光滑水平面上有质量均为m的A、B两物体,在水平面的右端有一轻弹簧,弹簧的右端固定在水平面右端的墙壁上,且A、B与弹簧在同一条水平线上,现给A向右的初速度v0使其向B运动并与B碰撞,碰后A、B粘在一起向弹簧运动,设在整个A、B与弹簧作用的过程中,弹簧都在弹性限度内,求弹簧在相互作用过程中的最大弹性势能Epm.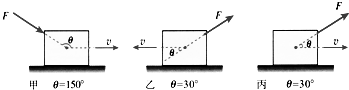 如图所示表示物体在力F作用下在水平面上发生一段位移L,则在以下三种情况下力F对物体所做的功分别是W甲=$10\sqrt{3}$J,W乙=-$10\sqrt{3}$J,W丙=$10\sqrt{3}$J.图(设在这三种情况下力、位移的大小相同:F=10N,L=2m)
如图所示表示物体在力F作用下在水平面上发生一段位移L,则在以下三种情况下力F对物体所做的功分别是W甲=$10\sqrt{3}$J,W乙=-$10\sqrt{3}$J,W丙=$10\sqrt{3}$J.图(设在这三种情况下力、位移的大小相同:F=10N,L=2m)