题目内容
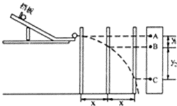
【题目】如图所示,竖直平面xOy内存在水平向右的匀强电场,场强大小E=10N/c,在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场,磁感应强度大小B=0.5T一带电量q= +0.2C、质量m=0.4kg的小球由长l=0.4m的细线悬挂于P点小球可视为质点,现将小球拉至水平位置A无初速释放,小球运动到悬点P正下方的坐标原点O时,悬线突然断裂,此后小球又恰好能通过O点正下方的N点,(g=10m/s2),求:
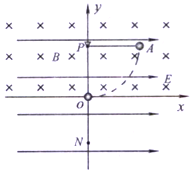
(1)小球运动到O点时的速度大小;
(2)悬线断裂前瞬间拉力的大小;
(3)ON间的距离。
【答案】(1)2m/s (2) 8.2N (3)3.2m
【解析】试题分析:由A到O的过程中,只有重力和电场力做功,根据动能定理即可求得O点的速度;在最低点时,绳的拉力、洛伦兹力和重力的合力提供向心力,根据牛顿第二定律即可求得拉力大小;悬线断裂后,沿电场方向小球做匀减速直线运动,沿重力方向做自由落体运动,小球又恰好能通过O点正下方的N点,说明小球到达N点时,沿电场方向的速度为vo,从而可求的由ON的时间,继而求出ON间的距离。
(1)小球从A运到O的过程中,根据动能定理: ![]()
代入数据求得小球在O点速度为:v0=2m/s
(2)小球运到O点绳子断裂前瞬间,对小球应用牛顿第二定律: ![]()
洛伦兹力: ![]()
联立解得:T=8.2N。
(3)绳断后,小球水平方向加速度![]()
小球从O点运动至N点所用时间为: ![]()
ON间距离为: ![]() 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目