题目内容
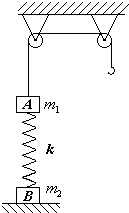（2005?山东）如图，质量为m1的物体A经一轻质弹簧与下方地面上的质量为m2的物体B相连，弹簧的劲度系数为k，A、B都处于静止状态．一条不可伸长的轻绳绕过轻滑轮，一端连物体A，另一端连一轻挂钩．开始时各段绳都处于伸直状态，A上方的一段绳沿竖直方向．现在挂钩上挂一质量为m3的物体C并从静止状态释放，已知它恰好能使B离开地面但不继续上升．若将C换成另一个质量为（m1十m3）的物体D，仍从上述初始位置由静止状态释放，则这次B刚离地时D的速度的大小是多少？已知重力加速度为g．分析：当挂一质量为m3的物体C时，恰好能使B离开地面但不继续上升，说明此时弹簧对B的拉力的大小恰好和B的重力相等，由此可以求得弹簧弹性势能的增加量，当换成另一个质量为（m1十m3）的物体D时，弹簧弹性势能的增加量是相同的，从而能可以求得B刚离地时D的速度的大小．
解答：解：开始时，A、B静止，设弹簧压缩量为x1，有
kx1=mlg ①
挂C并释放后，C向下运动，A向上运动，设B刚要离地时弹簧伸长量为x2，有
kx2=m2g ②
A不再上升，表示此时A和C的速度为零，C已降到其最低点．由机械能守恒，与初始状态相比，弹簧弹性势能的增加量为
△E=m3g（x1+x2）-m1g（x1+x2）③
C换成D后，当B 刚离地时弹簧势能的增量与前一次相同，由能量关系得
（m1+m3）V2+
m1V2=（m1+m3）g（x1+x2）-m1g（x1+x2）-△E ④
由③④式得
（2m1+m3）V2=m1g（x1+x2） ⑤
由①②⑤式得
V=
．
所以B刚离地时D的速度的大小是
．
kx1=mlg ①
挂C并释放后，C向下运动，A向上运动，设B刚要离地时弹簧伸长量为x2，有
kx2=m2g ②
A不再上升，表示此时A和C的速度为零，C已降到其最低点．由机械能守恒，与初始状态相比，弹簧弹性势能的增加量为
△E=m3g（x1+x2）-m1g（x1+x2）③
C换成D后，当B 刚离地时弹簧势能的增量与前一次相同，由能量关系得
| 1 |
| 2 |
| 1 |
| 2 |
由③④式得
| 1 |
| 2 |
由①②⑤式得
V=
|
所以B刚离地时D的速度的大小是
|
点评：前后两次的过程中，弹簧弹性势能的增加量是相同的，这是联系两个过程的过度量，由此来求解D的速度．
练习册系列答案
相关题目
（2005?山东）如图，在一水平放置的平板MN的上方有匀强磁场，磁感应强度的大小为B，磁场方向垂直于纸面向里．许多质量为m带电量为+q的粒子，以相同的速率v沿位于纸面内的各个方向，由小孔O射人磁场区域．不计重力，不计粒子间的相互影响．下列图中阴影部分表示带电粒子能经过区域，其中R=mv/qB．哪个图是正确的？（ ）
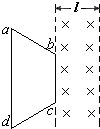（2005?山东）如图所示，两条平行虚线之间存在匀强磁场，虚线间的距离为l，磁场方向垂直纸面向里，abcd是位于纸面内的梯形线圈，ad与bc间的距离也为l，t=0时刻，bc边与磁场区域左边界重合．现令线圈以向右的恒定速度v沿垂直于磁场区域边界的方向穿过磁场区域，取沿a→b→c→d→a方向的感应电流为正，则在线圈穿越磁场区域的过程中，感应电流I随时间t变化的图线是（ ）
（2005?山东）如图所示，绝热隔板K把绝热的气缸分隔成体积相等的两部分，K与气缸壁的接触是光滑的．两部分中分别盛有相同质量、相同温度的同种气体a和b气体分子之间相互作用势能可忽略．现通过电热丝对气体a加热一段时闻后，a、b各自达到新的平衡，则（ ）