题目内容
19.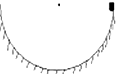 如图所示,一滑块从半圆形光滑轨道上端由静止开始滑下,当滑到最低点时,关于滑块动能大小和对轨道最低点的压力,下列结论正确的是( )
如图所示,一滑块从半圆形光滑轨道上端由静止开始滑下,当滑到最低点时,关于滑块动能大小和对轨道最低点的压力,下列结论正确的是( )| A. | 轨道半径越大,滑块动能越大,对轨道的压力越大 | |
| B. | 轨道半径越大,滑块动能越大,对轨道的压力与半径无关 | |
| C. | 轨道半径不变,滑块的质量越大,滑块动能越大,对轨道的压力越小 | |
| D. | 轨道半径不变,滑块的质量越大,滑块动能越大,对轨道的压力不变 |
分析 根据机械能守恒定律或动能定理得出小球运动到最低点的速度,根据牛顿第二定律求出最低点轨道对小球的支持力,从而得到球对轨道底端压力的大小与半径的关系
解答 解:对于物体下滑的过程,根据动能定理得:
mgR=$\frac{1}{2}$mv2,得:
v2=2gR.
物体到达最低点的动能为:
EK=$\frac{1}{2}$mv2=mgR,可见,质量越大,半径越大,动能越大.
在轨道最低点,由牛顿第二定律得,N-mg=m$\frac{{v}^{2}}{R}$,
解得:N=3mg.则知A、B两球对轨道的压力大小与半径也无关,只与重力有关.故B正确,ACD错误.
故选:B
点评 本题综合考查了动能定理和牛顿第二定律,关键掌握向心力的来源.本题中的结果要作为常识要记住.

练习册系列答案
相关题目
10. 如图所示,重为G的物体系在OA、OB两根等长的细绳上,细绳的A端固定,B端沿半圆支架从水平位置逐渐移至竖直位置C的过程中( )
如图所示,重为G的物体系在OA、OB两根等长的细绳上,细绳的A端固定,B端沿半圆支架从水平位置逐渐移至竖直位置C的过程中( )
 如图所示,重为G的物体系在OA、OB两根等长的细绳上,细绳的A端固定,B端沿半圆支架从水平位置逐渐移至竖直位置C的过程中( )
如图所示,重为G的物体系在OA、OB两根等长的细绳上,细绳的A端固定,B端沿半圆支架从水平位置逐渐移至竖直位置C的过程中( )| A. | OB绳上的弹力先减小后增大 | B. | OB绳上的弹力先增大后减小 | ||
| C. | OA绳上的弹力先减小后增大 | D. | OA绳上的弹力先增大后减小 |
7. 如图所示,Q1Q2为两个固定在绝缘水平面上的异性点电荷,其中Q1为负电荷,Q1的电荷量是Q2的四倍,它们相距L.在其连线上有一点P,P离Q2的距离为$\frac{L}{2}$.下列说法正确的是( )
如图所示,Q1Q2为两个固定在绝缘水平面上的异性点电荷,其中Q1为负电荷,Q1的电荷量是Q2的四倍,它们相距L.在其连线上有一点P,P离Q2的距离为$\frac{L}{2}$.下列说法正确的是( )
 如图所示,Q1Q2为两个固定在绝缘水平面上的异性点电荷,其中Q1为负电荷,Q1的电荷量是Q2的四倍,它们相距L.在其连线上有一点P,P离Q2的距离为$\frac{L}{2}$.下列说法正确的是( )
如图所示,Q1Q2为两个固定在绝缘水平面上的异性点电荷,其中Q1为负电荷,Q1的电荷量是Q2的四倍,它们相距L.在其连线上有一点P,P离Q2的距离为$\frac{L}{2}$.下列说法正确的是( )| A. | P右侧各点电场强度方向均向右 | |
| B. | 从P右侧到无穷远,各点电场强度依次是先变大后变小 | |
| C. | 从P右侧到无穷远,各点电势依次是先降低再升高 | |
| D. | 负电荷从P点沿两电荷连线向右移到无穷远,其电势能先增大后减小 |
11.一定质量的理想气体处于某一平衡状态,此时其压强为p0,有人设计了四种途径,使气体经过每种途径后压强仍为p0.下面四种途径中可能的途径是( )
| A. | 先等温膨胀,再等容降温 | B. | 先等温压缩,再等容降温 | ||
| C. | 先等容升温,再等温压缩 | D. | 先等容降温,再等温压缩 |
8. 如图所示,电荷量为Q1、Q2的两个正点电荷分别置于A点和B点,两点相距L,在以L为直径的光滑绝缘半圆环上,穿着一个带电荷量q的小球(视为点电荷,重力不计),小球恰好静止在P点,此时PA与AB的夹角α=37°.已知cos37°=0.8,sin37°=0.6.则Q1与Q2的大小关系为( )
如图所示,电荷量为Q1、Q2的两个正点电荷分别置于A点和B点,两点相距L,在以L为直径的光滑绝缘半圆环上,穿着一个带电荷量q的小球(视为点电荷,重力不计),小球恰好静止在P点,此时PA与AB的夹角α=37°.已知cos37°=0.8,sin37°=0.6.则Q1与Q2的大小关系为( )
 如图所示,电荷量为Q1、Q2的两个正点电荷分别置于A点和B点,两点相距L,在以L为直径的光滑绝缘半圆环上,穿着一个带电荷量q的小球(视为点电荷,重力不计),小球恰好静止在P点,此时PA与AB的夹角α=37°.已知cos37°=0.8,sin37°=0.6.则Q1与Q2的大小关系为( )
如图所示,电荷量为Q1、Q2的两个正点电荷分别置于A点和B点,两点相距L,在以L为直径的光滑绝缘半圆环上,穿着一个带电荷量q的小球(视为点电荷,重力不计),小球恰好静止在P点,此时PA与AB的夹角α=37°.已知cos37°=0.8,sin37°=0.6.则Q1与Q2的大小关系为( )| A. | Q1=$\frac{27}{64}$Q2 | B. | Q1=$\frac{64}{27}$Q2 | C. | Q1=$\frac{9}{16}$Q2 | D. | Q1=$\frac{16}{9}$Q2 |
 在利用单摆测定重力加速度的实验中
在利用单摆测定重力加速度的实验中 如图所示气垫是常用的一种实验仪器,它是利用气泵使带孔的导轨与滑块之间形成气垫,使滑块悬浮在轨道上,滑块在轨道上的运动可视为没有摩擦.我们可以用带竖直挡板C和D的气垫轨道以及滑块A和B来验证动量守恒定律,实验装置如图所示(弹簧的长度忽略不计),采用的实验步骤如下:
如图所示气垫是常用的一种实验仪器,它是利用气泵使带孔的导轨与滑块之间形成气垫,使滑块悬浮在轨道上,滑块在轨道上的运动可视为没有摩擦.我们可以用带竖直挡板C和D的气垫轨道以及滑块A和B来验证动量守恒定律,实验装置如图所示(弹簧的长度忽略不计),采用的实验步骤如下: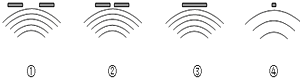 各图分别表示一列水波在传播过程中遇到了小孔(①、②图)或障碍物(③、④图),每两条相邻(图中曲线)之间距离表示一个波长,其中能发生明显衍射现象的有( )
各图分别表示一列水波在传播过程中遇到了小孔(①、②图)或障碍物(③、④图),每两条相邻(图中曲线)之间距离表示一个波长,其中能发生明显衍射现象的有( )