题目内容
【题目】如图所示，光滑水平面OB与足够长的粗糙斜面BC相接于B点，O端有一竖直墙面，一轻弹簧左端固定于竖直墙面，现用质量为m1的滑块压缩弹簧至D点，然后由静止释放，滑块脱离弹簧后经B点滑上斜面，上升到最大高度，并静止在斜面上，不计滑块在B点的机械能损失．若换用相同材料、相同粗糙程度、质量为m2（m2＞m1） 的滑块压缩弹簧至同一点D后，重复上述过程，下列说法正确的是（ ）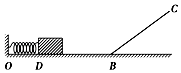
A.两滑块到达B点的速度相同
B.两滑块沿斜面上升的最大高度相同
C.两滑块上升到最高点的过程中克服重力做功相同
D.m2上升到最高点的后会滑下来
【答案】C
【解析】解：A、换用质量为m2的滑块压缩弹簧至同一点D时，弹簧具有的弹性势能相等，根据能量守恒定律知，两滑块到B点时的动能相同，由于质量不同，则速度不同，故A错误；
B、两滑块在斜面上运动时加速度相同，由于初速度不同，故上升高度不同．故B错误；
C、两滑块上升到最高点过程克服重力做的功表达式WG=mgh，对任一滑块（质量设为m），由能量守恒定律得：EP=mgh+μmgcosθ× 
，所以 WG=mgh= 
，故两滑块上升到最高点过程克服重力做的功相同，故C正确；
D、对于m1上升到最高点时有m1gsinθ≤μm1gcosθ，即 sinθ≤μcosθ，该式与滑块的质量无关，所以m2上升到最高点后也静止在斜面上，故D错误．
故选：C
【考点精析】通过灵活运用功能关系和能量守恒定律，掌握当只有重力（或弹簧弹力）做功时，物体的机械能守恒；重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2；合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 （动能定理）；除了重力（或弹簧弹力）之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1；能量守恒定律：能量既不会消灭，也不会创生，它只会从一种形式转化为其他形式，或者从一个物体转移到另一个物体，而在转化和转移过程中，能量的总量保持不变即可以解答此题．
