题目内容
如图,质量m=2.5kg的物体A,在水平推力F的作用下,恰能沿倾角为θ=37°的斜面匀速上滑,g取10m/s2。(sin37°=0.6,cos37°=0.8)
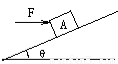
(1)若A与斜面间动摩擦数为μ=0.5,求F。
(2)若斜面是光滑的,推力F=15N,方向为平行斜面向上,为使A在斜面上运动的加速度大小小于1m/s2,求倾角的正弦值sinθ的范围。
(1)50N; (2)0.5<sinθ<0.7
【解析】
试题分析:(1) 物体m受力如图,把F,mg沿斜面和垂直斜面进行分解.
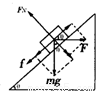
沿斜面方向受力平衡得:f+mgsinθ=Fcosθ
在垂直斜面方向受力平衡得:FN=mgcosθ+Fsinθ
由滑动摩擦力公式:f=μFN
综合上述,代入数值得:F=50N
(2)沿斜面方向合力F合=F- mgsinθ=ma
A在斜面上运动的加速度大小小于1m/s2 故 -1m/s2<a<+1m/s2
代入数值得:0.5<sinθ<0.7
考点:牛顿第二定律

某小组“验证牛顿第二定律”的实验装置如下图,长木板固定在水平桌面上,一端装有定滑轮;木板上有一滑块,其一端与电磁打点计时器的纸带相连,另一端通过跨过定滑轮的细线与托盘连接。
(1)该小组研究加速度和拉力关系时,得到的图象将会是图

(2)下图给出的是实验中获取的一条纸带的一部分:1、2、3、4、5、6、7是计数点每相邻两计数点间还有4个打点(图中未标出),计数点间的距离如图所示。根据图中数据计算的加速度a= m/s2 (保留三位有效数字)。

(3)某同学在研究加速度和质量关系时,记录下如下数据,请在下面的坐标纸中选择合理的坐标,描出相关图线,并可以由图线可以得到实验结论: 。
次数 | 1 | 2 | 3 | 4 | 5 |
质量m/g | 200 | 300 | 400 | 500 | 600 |
加速度a/m˙s-2 | 1.00 | 0.67 | 0.50 | 0.40 | 0.33 |