题目内容
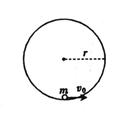
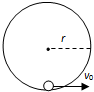 如图所示,在一固定的竖直光滑圆弧轨道内部的最低点,静止有一个可视为质点的小球,已知地球表面的重力加速度为g,圆弧轨道的半径为r,则为了使小球能在竖直平面内运动且不脱离圆弧轨道,求小球的初速度v0应该满足的条件?
如图所示,在一固定的竖直光滑圆弧轨道内部的最低点,静止有一个可视为质点的小球,已知地球表面的重力加速度为g,圆弧轨道的半径为r,则为了使小球能在竖直平面内运动且不脱离圆弧轨道,求小球的初速度v0应该满足的条件?分析:要使小球不脱离轨道运动,1、越过最高点.2、不越过四分之一圆周.根据动能定理求出初速度v0的条件.
解答:解:若小球恰好经过最高点时,重力提供向心力,根据向心力公式得:
mg=m
解得:v=
小球从最低点运动到最高点的过程中,根据动能定理得:
mv2-
mv02=-mg?2r
解得:v0=
若不通过四分之一圆周,根据动能定理有:
-mgr=0-
mv02
解得:v0=
所以小球的初速度v0应大于等于
或者小于等于
.
答:小球的初速度v0应该满足的条件为v0≥
或v0≤
.
mg=m
| v2 |
| r |
解得:v=
| gr |
小球从最低点运动到最高点的过程中,根据动能定理得:
| 1 |
| 2 |
| 1 |
| 2 |
解得:v0=
| 5gr |
若不通过四分之一圆周,根据动能定理有:
-mgr=0-
| 1 |
| 2 |
解得:v0=
| 2gr |
所以小球的初速度v0应大于等于
| 5gr |
| 2gr |
答:小球的初速度v0应该满足的条件为v0≥
| 5gr |
| 2gr |
点评:本题主要考查了向心力公式及动能定理的直接应用,知道小球恰好经过最高点时,重力提供向心力,根据向心力公式可以求出最高点的最小速度,难度不大,属于基础题.

练习册系列答案
相关题目
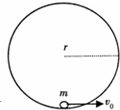 宇航员在月球表面完成下面实验:如图所示,在一固定的竖直光滑圆弧轨道内部最低点静止一质量为m的小球(可视为质点),当给小球一水平初速度v时,刚好能使小球在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,月球半径为R,引力常量为G.若在月球表面上发射一颗环月卫星,则所需的最小发射速度为多大?
宇航员在月球表面完成下面实验:如图所示,在一固定的竖直光滑圆弧轨道内部最低点静止一质量为m的小球(可视为质点),当给小球一水平初速度v时,刚好能使小球在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,月球半径为R,引力常量为G.若在月球表面上发射一颗环月卫星,则所需的最小发射速度为多大? 时,小球刚好能在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,月球的半径为R,引力常量为G.
时,小球刚好能在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,月球的半径为R,引力常量为G.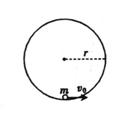
 时,小球刚好能在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,月球的半径为R,引力常量为G.
时,小球刚好能在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,月球的半径为R,引力常量为G.