题目内容
甲、乙两球分别以半径R1、R2做匀速圆周运动，两球质量M甲=2M乙，圆半径R甲=R乙/3，甲球每分钟转30周，乙球每分钟转20周，则甲、乙两球所受向心力大小之比为（ ）
分析：先根据ω=
求解角速度之比，然后根据Fn=mω2r求解向心力大小之比．
| △θ |
| △t |
解答：解：甲球每分钟转30周，乙球每分钟转20周，根据ω=
，其角速度之比为3：2；
两球质量M甲=2M乙，圆半径R甲=
R乙，根据Fn=mω2r，甲、乙两球所受向心力大小之比为：
=
=
×(
)2×
=
；
故选B．
| △θ |
| △t |
两球质量M甲=2M乙，圆半径R甲=
| 1 |
| 3 |
| F甲 |
| F乙 |
m甲
| ||
| m乙ω2r乙 |
| 2 |
| 1 |
| 3 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
故选B．
点评：本题关键是根据角速度定义求解角速度之比，然后根据向心力公式求解向心力之比，记住公式是关键．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
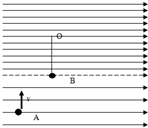如图，虚线下方有足够大的场强大小E=5.0×103 V/m和上方场强为8mg/3q的匀强电场，方向均水平向右．质量均为m=1.5×10-2kg的A、B小球，其中B球为绝缘小球且不带电，被长为R的绝缘丝线悬挂在O点刚好静止在虚线上，A球带电荷量为qA=+6.0×10-6C，在竖直平面内的以某一初速度v竖直进入电场，运动到B点速度刚好水平，同时与B球发生正碰并立即粘在一起围绕O点做半径为R=0.7m完整的圆周运动，假设甲、乙两球可视为质点，g取10m/s2．（sin53°=0.8，c0s53°=0.6）
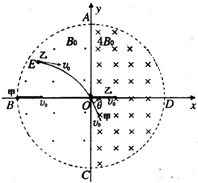光滑绝缘水平面上有甲、乙、丙三个很小的金属球，质量均为m，甲不带电，乙带电量为+q，丙带电量为+
