题目内容
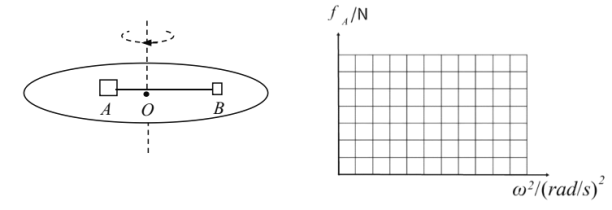
【题目】如图所示,在水平圆盘上,沿半径方向放置物体A和B,mA=4kg,mB=1kg,它们分居在圆心两侧,与圆心距离为rA=0.1m,rB=0.2m,中间用细线相连,A、B与盘间的动摩擦因数均为μ=0.2,设最大静摩擦力等于滑动摩擦力,若圆盘从静止开始绕中心转轴非常缓慢地加速转动,用![]() 表示圆盘转动的角速度,
表示圆盘转动的角速度,![]() 表示物体A与圆盘之间的摩擦力,g=10m/s2。
表示物体A与圆盘之间的摩擦力,g=10m/s2。
(1)细线中出现张力时,圆盘转动的角速度![]() 1;
1;
(2)A、B两物体相对圆盘将要滑动时,圆盘转动的角速度![]() 3;
3;
(3)在下列坐标图中分别画出A、B两物体滑动前,![]() 随
随![]() 变化的关系图像;
变化的关系图像;
【答案】(1)![]() (2)
(2)![]() rad/s(3)
rad/s(3)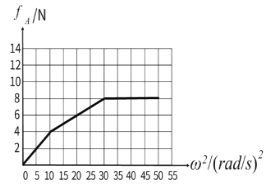
【解析】
解:(1)运动开始,两个物块的向心力各由圆盘对他们的摩擦力提供,则有:![]()
![]()
绳子拉力:![]()
随着圆盘转速的增加,当![]() 达到
达到![]() 时,物块B达到最大静摩擦力,则有:
时,物块B达到最大静摩擦力,则有:![]()
解得: ![]()
(2)随后,绳子有拉力![]()
![]() 物块:
物块: ![]()
![]() 物块:
物块: ![]()
解得:![]()
当![]() 时,
时,![]() ,
, ![]()
当![]() 时,绳子的拉力持续增大,以提供两个物体的向心力,此时,
时,绳子的拉力持续增大,以提供两个物体的向心力,此时,![]() 的摩擦力是最大静摩擦力,物块
的摩擦力是最大静摩擦力,物块![]() 所受到的摩擦力逐渐减小,直至反向最大
所受到的摩擦力逐渐减小,直至反向最大
当![]() 时,对
时,对![]() :
:![]()
对![]() :
:![]()
解得:![]()
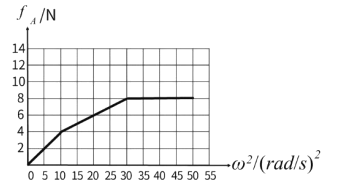
(3)综上所述![]() 随
随![]() 变化的分段函数为
变化的分段函数为
![]() 0≤
0≤![]() ≤
≤![]() rad/s
rad/s
![]()
![]() ≤
≤![]() ≤
≤![]() rad/s
rad/s
![]()
![]() ≤
≤![]() ≤
≤![]() rad/s
rad/s

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目