题目内容
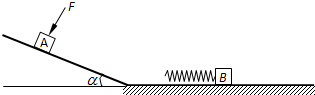
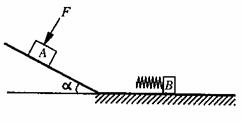
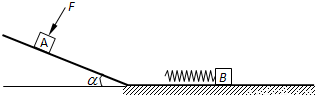
如图所示，粗糙斜面其倾角为
，底端通过长度可忽略的光滑小圆弧与光滑水平面连接，A、B是两个质量均为m=1kg的小滑块（可视为质点），B的左端连有轻质弹簧，处于静止状态。当滑块A置于斜面上且受到大小F=4N，方向垂直斜面向下的恒力作用时，恰能沿斜面向下匀速运动。现撤去F，让滑块A从斜面上距斜面底端L=1m处由静止开始下滑，若取g=10m/s2,sin=0.6,cos=0.8。求：
（1）滑块A与斜面的动摩擦因数
；
（2）滑块A到达斜面底端时的速度大小v1；
（3）滑块A在斜面上运动的加速度大小；
（4）滑块A开始与弹簧接触，到此后两滑块和弹簧构成的系统在相互作用过程中，弹簧的最大弹性势能
。
解：（1）滑块A匀速下滑时，受重力mg、恒力F、斜面支持力FN和摩擦力F
作用，由平衡条件有 mgsin
=FN①
FN=mgcos+F②
联立①②并化简后得
③
代入数据解得动摩擦因数
撤去F后，滑块A沿斜面匀加速下滑，由动能定理有：
④
代入数据得：
⑤
（3）根据牛顿第二定律
有
⑥
代入数据得=2m/s2
（4）两滑块和弹簧构成的系统在相互作用过程中动量守恒，当它们速度相等时，弹簧具有最大弹性势能，设共同速度为v2，由动量守恒和能量守恒定律有：
⑦ 
⑧
联立⑤⑦⑧式解得Ep=1J
练习册系列答案
智能训练练测考系列答案
相关题目
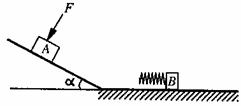
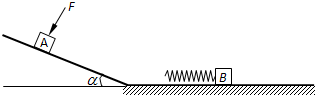如图所示，粗糙斜面其倾角为α，底端通过长度可忽略的光滑小圆弧与光滑水平面连接．．A、B是两个质量均为 m=1㎏的小滑块（可视为质点），B的左端连有轻质弹簧，处于静止状态．当滑块A置于斜面上且受到大小F=4N，方向垂直斜面向下的恒力作用时，恰能沿斜面向下匀速运动．现撤去F，让滑块A从斜面上距斜面底端L=1m处由静止开始下滑，若取g=10m/s2，sinα=0.6，cosα=0.8．求：
，底端通过长度可忽略的光滑小圆弧与光滑水平面连接，A、B是两个质量均为m=1kg的小滑块（可视为质点），B的左端连有轻质弹簧，处于静止状态。当滑块A置于斜面上且受到大小F=4N，方向垂直斜面向下的恒力作用时，恰能沿斜面向下匀速运动。现撤去F，让滑块A从斜面上距斜面底端L=1m处由静止开始下滑，若取g=10m/s2,sin
；
。
