题目内容
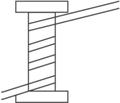
如图4-6-11所示,ad、bd、cd是竖直面内三根固定的光滑细杆,a、b、c、d位于同一圆周上,a点为圆周的最高点,d点为最低点.每根杆上都套着一个小滑环(图中未画出),三个滑环分别从a、b、c处释放(初速为0),用t1、t2、t3依次表示各滑环到达d所用的时间,则( )?
图4-6-11
? A.t1<t2<t3? ? B.t1>t2>t3?
? C.t3>t1>t2? ? D.t1=t2=t3?
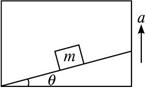
解析:设杆与水平方向的夹角为θ,则对小滑环,由牛顿第二定律可得?
mgsinθ=ma ①?
由几何关系,细杆长度L=2Rsinθ ②?
而小滑环在杆上有静止匀加速下滑,由运动学公式有L=![]() at2 ③?
at2 ③?
联立①②③解得t=2![]() .由此不难看出t1=t2=t3.?
.由此不难看出t1=t2=t3.?
答案:D

练习册系列答案
相关题目