题目内容
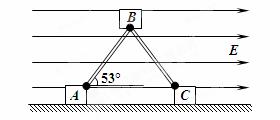
如图所示，两个长均为L的轻质杆，通过A、B、C上垂直纸面的转动轴与A、B、C三个物块相连，整体处于竖直面内。A、C为两个完全相同的小物块，B物块的质量与A小物块的质量之比为2∶1，三个物块的大小都可忽略不计。A、C两物块分别带有+q、-q的电量，并置于绝缘水平面上，在水平面上方有水平向右的匀强电场，场强为E，物块间的库仑力不计。当AB、BC与水平面间的夹角均为53°时，整体恰好处于静止状态，一切摩擦均不计，并且在运动过程中无内能产生，重力加速度为g。（sin53°=0.8，cos53°=0.6）
（1）求B物块的质量；
（2）在B物块略向下移动一些，并由静止释放后，它能否到达水平面？如果能，请求出B物块到达地面前瞬时速度的大小；如果不能，请求出B物块所能到达的最低位置。
答案：⑴
⑵
解析：（1） 以A为研究对象，如图1所示，N为轻质杆的弹力大小，则有N cos53°= Eq，得：N =
，
以B为研究对象，如图2所示，Mg为大物块的重力，则有2N sin53°= Mg，得：
。
（2）B物块将向下做加速度增大的加速运动，一直到B物体落地；
以整体为研究对象，有重力和电场力做功，设大物块落地前的瞬间速度大小为v，此时小物块的速度为零，即：
，得：
。
练习册系列答案
相关题目
如图所示，两个重量均为1N的相同木块跟两个原长均为10cm、劲度系数均为100N/m的相同轻弹簧拴接在一起，竖直放在水平地面上，两木块均处于静止状态．则上面的木块距离地面的高度是（ ）
如图所示，两个质量均为m的小环套在一水平放置的粗糙长杆上，两根长度均为l的轻绳一端系在小环上，另一端系在质量为M的木块上，两个小环之间的距离也为l，小环恰保持静止．试求：
