题目内容
19.已知某星球质量是地球的2倍,半径是地球的0.5倍,求该星球的第一宇宙速度和该星球表面的重力加速度?(已知地球第一宇宙速度是7.9m/s,重力加速度g=10m/s2)分析 根据万有引力提供圆周运动向心力,求出第一宇宙速度的表达式,根据万有引力等于重力,得到星球表面重力加速度的表达式,再结合星球与地球半径和质量的关系求解即可.
解答 解:第一宇宙速度是近地卫星的环绕速度,由万有引力提供向心力得:G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$,
解得:v=$\sqrt{\frac{GM}{R}}$;
该星球的第一宇宙速度与地球的第一宇宙速度之比:
$\frac{{v}_{星}}{{v}_{地}}$=$\frac{\sqrt{\frac{G{M}_{星}}{{R}_{星}}}}{\sqrt{\frac{G{M}_{地}}{{R}_{地}}}}$=$\sqrt{\frac{2}{1}×\frac{2}{1}}$=2,
所以该星球的第一宇宙速度:v星=2v地=15.8km/s
在天体表面上,由重力等于万有引力,即:mg=G$\frac{Mm}{{R}^{2}}$,解得:g=$\frac{GM}{{R}^{2}}$,
则得星球表面的重力加速度与地球表面的重力加速度之比:
$\frac{{g}_{星}}{{g}_{地}}$=$\frac{\frac{G{M}_{星}}{{R}_{星}^{2}}}{\frac{G{M}_{地}}{{R}_{地}^{2}}}$=$\frac{2}{1}×\frac{{2}^{2}}{1}$=8
该星球表面的重力加速度:g星=8g=80m/s2;
答:该星球的第一宇宙速度为15.8km/s,该星球表面的重力加速度是80m/s2.
点评 本题关键是根据第一宇宙速度的表达式列式求解,其中第一宇宙速度为贴近星球表面飞行的卫星的环绕速度.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
9.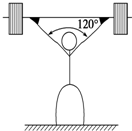 举重运动员在抓举比赛时,为了减小杠铃上升的高度和便于发力,抓握杠铃的两手间要有较大距离,使两臂上举后两臂间成钝角,手臂伸直后所受作用力沿手臂方向,一质量为75kg的运动员,在举起125kg的杠铃时,两臂成120°角,如图所示,则此时运动员的每只手臂对杠铃的作用力F及运动员对地面的压力FN的大小分别为(g取10m/s2)( )
举重运动员在抓举比赛时,为了减小杠铃上升的高度和便于发力,抓握杠铃的两手间要有较大距离,使两臂上举后两臂间成钝角,手臂伸直后所受作用力沿手臂方向,一质量为75kg的运动员,在举起125kg的杠铃时,两臂成120°角,如图所示,则此时运动员的每只手臂对杠铃的作用力F及运动员对地面的压力FN的大小分别为(g取10m/s2)( )
 举重运动员在抓举比赛时,为了减小杠铃上升的高度和便于发力,抓握杠铃的两手间要有较大距离,使两臂上举后两臂间成钝角,手臂伸直后所受作用力沿手臂方向,一质量为75kg的运动员,在举起125kg的杠铃时,两臂成120°角,如图所示,则此时运动员的每只手臂对杠铃的作用力F及运动员对地面的压力FN的大小分别为(g取10m/s2)( )
举重运动员在抓举比赛时,为了减小杠铃上升的高度和便于发力,抓握杠铃的两手间要有较大距离,使两臂上举后两臂间成钝角,手臂伸直后所受作用力沿手臂方向,一质量为75kg的运动员,在举起125kg的杠铃时,两臂成120°角,如图所示,则此时运动员的每只手臂对杠铃的作用力F及运动员对地面的压力FN的大小分别为(g取10m/s2)( )| A. | F=1 250 N,FN=2 000 N | B. | F=1 250 N,FN=3 250 N | ||
| C. | F=625 N,FN=2 000 N | D. | F=722 N,FN=2 194 N |
10.关于位移和路程,下列说法中正确的是( )
| A. | 出租车是按位移的大小来计费的 | |
| B. | 出租车是按路程的大小来计费的 | |
| C. | 在田径场1500m长跑比赛中,跑完全程的运动员的位移大小为1500m | |
| D. | 高速公路路牌上显示“银川120km”,表示该处到银川的位移大小为120km |
7.截面直径为d、长为L的导线,两端电压为U,当这三个量中的一个改变时,对自由电子定向移动平均速率的影响,下列说法正确的是( )
| A. | 电压U加倍时,自由电子定向移动的平均速率不变 | |
| B. | 导线长度L加倍时,自由电子定向移动的平均速率减为原来的一半 | |
| C. | 导线截面直径d加倍时,自由电子定向移动的平均速率增加一倍 | |
| D. | 导线截面直径d加倍时,自由电子定向移动的平均速率加倍 |
14. 如图所示,两根轻弹簧下面均连接一个质量为m的小球,上面一根弹簧的上端固定在天花板上,两小球之间通过一不可伸长的细线相连接,细线受到的拉力大小等于4mg.当剪断两球之间的细线瞬间,以下关于球A的加速度大小aA;球B的加速度大小aB;以及弹簧对天花板的拉力大小正确的是( )
如图所示,两根轻弹簧下面均连接一个质量为m的小球,上面一根弹簧的上端固定在天花板上,两小球之间通过一不可伸长的细线相连接,细线受到的拉力大小等于4mg.当剪断两球之间的细线瞬间,以下关于球A的加速度大小aA;球B的加速度大小aB;以及弹簧对天花板的拉力大小正确的是( )
 如图所示,两根轻弹簧下面均连接一个质量为m的小球,上面一根弹簧的上端固定在天花板上,两小球之间通过一不可伸长的细线相连接,细线受到的拉力大小等于4mg.当剪断两球之间的细线瞬间,以下关于球A的加速度大小aA;球B的加速度大小aB;以及弹簧对天花板的拉力大小正确的是( )
如图所示,两根轻弹簧下面均连接一个质量为m的小球,上面一根弹簧的上端固定在天花板上,两小球之间通过一不可伸长的细线相连接,细线受到的拉力大小等于4mg.当剪断两球之间的细线瞬间,以下关于球A的加速度大小aA;球B的加速度大小aB;以及弹簧对天花板的拉力大小正确的是( )| A. | 0;2g;2mg | B. | 4g;4g;2mg | C. | 4g;2g;4mg | D. | 0;4g;4mg |
8.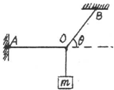 图中重物的质量为m,轻细线AO和BO的A、B端是固定的,平衡时AO是水平的,BO与水平面的夹角为θ,AO的拉力F1和BO的拉力F2的大小是( )
图中重物的质量为m,轻细线AO和BO的A、B端是固定的,平衡时AO是水平的,BO与水平面的夹角为θ,AO的拉力F1和BO的拉力F2的大小是( )
 图中重物的质量为m,轻细线AO和BO的A、B端是固定的,平衡时AO是水平的,BO与水平面的夹角为θ,AO的拉力F1和BO的拉力F2的大小是( )
图中重物的质量为m,轻细线AO和BO的A、B端是固定的,平衡时AO是水平的,BO与水平面的夹角为θ,AO的拉力F1和BO的拉力F2的大小是( )| A. | F1=mgcosθ | B. | F1=mgtanθ | C. | F2=mgsinθ | D. | F2=$\frac{mg}{sinθ}$ |
9.某电梯上升的速度图象如图所示,则( )


| A. | 前2s的平均速度是60m/s | B. | 第4s末的速度是60m/s | ||
| C. | 整过程的平均速度是45m/s | D. | 第6s末至第8s末电梯下降 |
