题目内容
【题目】如图所示,竖直放置的U形管左端封闭,右端开口,左、右两管的横截面积均为S=2cm2,在左管内用水银封闭一段长为l1=15cm、温度为T1=300K的空气柱(可看成理想气体),左右两管水银面高度差为h=15cm,外界大气压为P0=75cmHg.(玻璃管和水银柱都足够长)
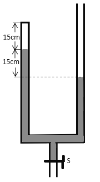
(1)若向右管中缓慢注入水银,直至两管水银面相平(注入水银过程中可认为气体温度不变),求在右管中注入水银的体积V;(以cm3为单位)
(2)在两管水银面相平后,缓慢升高气体的温度,直至封闭空气柱的长度为开始的长度,求此时空气柱的温度T。
(3)保持(2)的温度T不变,若将阀门S打开,缓慢流出部分水银,然后关闭阀门S,右管水银面下降了H=48cm,求左管水银面下降的高度。
【答案】(1)![]() ;(2)405K;(3)12cm
;(2)405K;(3)12cm
【解析】
(1)封闭气体初始压强 ![]()
缓慢注入水银至两管水银面相平后气体压强![]()
由于温度不变,由玻意耳定律有![]()
解得:l2=12cm
加入水银的长度x=h+2(l1-l2)=21cm
解得加入水银的体积V=Sx=42cm3
(2)空气柱的长度变为开始的长度l1时,左管水银柱下降![]()
右管水银柱会上升3cm,此时气体的压强![]()
初始温度T1=300K,封闭气体从初始状态到最终状态,可以看作等容变化,
由查理定律 ![]()
解得:T=405K
(3)设左管水银面下降的高度x,则空气柱的长度l4=l1+ x=15+x,
左右管水银面的高度差y=H-x-2h=42-x
由于温度不变,由玻意耳定律有:![]()
联立解得:x=12cm

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目