Question

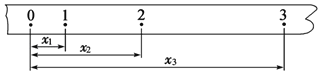
【题目】如图所示，在同一水平面上放置平行长直导轨，导轨I部分相距L＝0.4 m，导轨II部分相距L／2，其上平行静止地分别放置可在导轨上无摩擦滑动的金属棒ab和cd，两棒质量均为m＝0.1 kg，电阻均为R＝1 ，棒与导轨接触良好，导轨电阻不计，导轨处于磁场方向竖直向下，大小为B＝1 T的匀强磁场中，现使金属棒ab以v0＝10 m / s的初速向右开始运动，问：

（1）cd棒的最大加速度多大？

（2）若ab棒在导轨I部分时，cd棒已趋于稳定速度，求此时cd棒的稳定速度多大？

（3）在cd棒趋于稳定速度后，ab棒进入导轨II部分运动，则ab棒在滑行过程中还能产生的热量是多少？

（4）在cd棒趋于稳定速度后，ab棒恰进入导轨II部分时，令cd棒突然停止运动，ab棒继续运动直至停止的过程中，通过其横截面的电量为1 c，那么，ab棒在导轨上滑行的最大距离是多少？(假设两棒一直没有相碰)

Answer 1

【答案】1）4m/s2

2）4m/s

3）0.033J

4）7.5m

【解析】试题分析：ab棒刚起动时cd棒有最大加速，牛顿第二定律求出加速度；当杆稳定时磁通量变化量为零，应用动量定理求出速度；运动过程中两棒总动量守恒，应用能量守恒可得产生的热量，根据电量的表达式： ，求出位移。

（1）ab棒刚起动时cd棒有最大加速，此时感应电动势为：

感应电流为：

联立并代入数据解得：

cd所受安培力产生加速度： ，

最大加速度为：

（2）当cd棒趋于稳定速度时，此时有2vab＝vcd，由I相同得Fab＝2Fcd，

根据动量定理得:Fabt＝mv0－m vab ，Fcdt＝mvcd－0

联立以上可得： ，

（3）运动过程中两棒总动量守恒:mvab＋mvcd＝2mv， 代入数据解得：v＝3m/ s，

回路总热量为：

ab棒的热量为：

（4）ab棒在运动过程中产生的电动势为：

通过的电荷量为：

代入数据解得：