题目内容
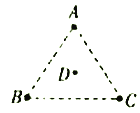
【题目】由多颗星体构成的系统，叫做多星系统。有这样一种简单的四星系统：质量刚好都相同的四个星体A、B、C、D，A、B、C分别位于等边三角形的三个顶点上，D位于等边三角形的中心。在四者相互之间的万有引力作用下，D静止不动，A、B、C绕共同的圆心D在等边三角形所在的平面内做相同周期的圆周运动。若四个星体的质量均为m，三角形的边长为a，引力常量为G，则下列说法正确的是
A. ABC三个星体做圆周运动的半径均为
B. A、B两个星体之间的万有引力大小为
C. A、B、C三个星体做圆周运动的向心加速度大小均为
D. A、B、C三个星体做圆周运动的周期均为
【答案】BC
【解析】
A.A、B、C绕中点D做圆周运动，由几何关系知：它们的轨道半径为：r=
a，故A错误；
B. 根据万有引力公式，A、B两个星体之间的万有引力大小为
，故B错误；
C.以A为研究对象，受到的合力为F=
，根据牛顿第二定律，F=ma，a=
，故C正确；
D.根据合力提供向心力有：
，得星体做圆周运动的周期为：T=
，故D错误。
故选：C
练习册系列答案
相关题目
