题目内容
3. 质谱仪原理如图所示,a为粒子加速器,电压为U1;b为速度选择器,磁场与电场正交,磁感应强度为B1,板间距离为d;c为偏转分离器,磁感应强度为B2.今有一质量为m、电荷量为+e的正电子(不计重力),经加速后,该粒子恰能通过速度选择器,粒子进入分离器后做半径为R的匀速圆周运动.求:
质谱仪原理如图所示,a为粒子加速器,电压为U1;b为速度选择器,磁场与电场正交,磁感应强度为B1,板间距离为d;c为偏转分离器,磁感应强度为B2.今有一质量为m、电荷量为+e的正电子(不计重力),经加速后,该粒子恰能通过速度选择器,粒子进入分离器后做半径为R的匀速圆周运动.求:(1)粒子射出加速器时的速度v为多少?
(2)速度选择器的电压U2为多少?
(3)粒子在B2磁场中做匀速圆周运动的半径R为多大?
分析 (1)根据动能定理qU1=$\frac{1}{2}$mv2求出粒子的速度v.
(2)在速度选择器中作匀速直线运动,电场力与洛仑兹力平衡,根据Eq=qvB1求出电压U2.
(3)根据洛仑兹力提供向心力,qvB2=$\frac{m{v}^{2}}{R}$,求出粒子在B2磁场中做匀速圆周运动的半径R.
解答 解:(1)粒子经加速电场U1加速,获得速度为v,由动能定理可知:
eU1=$\frac{1}{2}$mv2
解得v=$\sqrt{\frac{2{U}_{1}e}{m}}$
(2)在速度选择器中作匀速直线运动,电场力与洛仑兹力平衡得:eE=evB1
即$\frac{{U}_{2}}{d}e=ev{B}_{1}$
解得:U2=B1dv=B1d$\sqrt{\frac{2{U}_{1}e}{m}}$
(3)在B2中作圆周运动,洛仑兹力提供向心力,qvB2=m$\frac{{v}^{2}}{R}$
解得:R=$\frac{mv}{e{B}_{2}}=\frac{1}{{B}_{2}}\sqrt{\frac{2{U}_{1}m}{e}}$
答:(1)粒子射出加速器时的速度v为$\sqrt{\frac{2{U}_{1}e}{m}}$;
(2)速度选择器的电压B1d$\sqrt{\frac{2{U}_{1}e}{m}}$;
(3)粒子在B2磁场中做匀速圆周运动的半径为$\frac{1}{{B}_{2}}\sqrt{\frac{2{U}_{1}m}{e}}$.
点评 解决本题的关键掌握带电粒子在电场中的运动特点与在磁场中的运动特点,以及知道在速度选择器中作匀速直线运动,电场力与洛仑兹力平衡.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
13.关于电场强度和电势的概念,下列说法中正确的是( )
| A. | 电场中场强相等的点,其电势一定相等 | |
| B. | 电场中电势相等的点,其场强一定相等 | |
| C. | 电势为零的地方,场强一定为零 | |
| D. | 电势为零的地方,场强不一定为零 |
14. 如图所示,O1O2是矩形导线框abcd的对称轴,其左方有匀强磁场.以下对感应电流方向判断正确的是( )
如图所示,O1O2是矩形导线框abcd的对称轴,其左方有匀强磁场.以下对感应电流方向判断正确的是( )
 如图所示,O1O2是矩形导线框abcd的对称轴,其左方有匀强磁场.以下对感应电流方向判断正确的是( )
如图所示,O1O2是矩形导线框abcd的对称轴,其左方有匀强磁场.以下对感应电流方向判断正确的是( )| A. | 将abcd 向纸外平移,顺时针 | B. | 将abcd向右平移,顺时针 | ||
| C. | 将abcd以ab为轴转动60°,逆时针 | D. | 将abcd以cd为轴转动60°,逆时针 |
11.如果在某电场中将5.0×10-8C的电荷由A点移到B点,电场力做功为6.0×10-3J,那么( )
| A. | A、B两点间的电势差是1.2×105V | |
| B. | A、B两点间的电势差是3.0×10-10V | |
| C. | 若在A、B两点间移动2.5×10-8C的电荷,电场力将做7.5×10-18J的功 | |
| D. | 若在A、B两点间移动1.0×10-7C的电荷,电场力将做3.0×10-17J的功 |
15.如图所示为两个单摆的振动图象,若两单摆所在的位置的重力加速度相同,则他们的( )
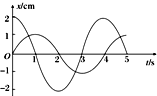

| A. | 摆球质量相等 | B. | 振幅相等 | ||
| C. | 摆长相等 | D. | 摆球同时改变速度方向 |


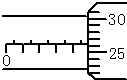 在测量金属丝电阻率的实验中:
在测量金属丝电阻率的实验中: