题目内容
如图所示，AB、AC为不可伸长的轻绳，小球质量为m="0.4" kg．当小车静止时，AC水平，AB与竖直方向夹角为θ=37°，试求小车分别以下列加速度向右匀加速运动时，两绳上的张力FAC、FAB分别为多少．（取g="10" m／s2。sin370=0.6,cos370=0.8） (1)a1="5" m／s2。 (2)a2="10" m／s2。
（1）FAB=5N FAC="1N" （2）5.7N
解析试题分析：设绳AC水平且拉力刚好为零时，临界加速度为a0
据牛顿第二定律
FABsin
=ma0 ①
FABcos="mg" ②
联立①、②两式并代入数据得 a0=7.5m/s2
（1）当a1=5m/s2< a0，此时AC绳伸直且有拉力。
据牛顿第二定律
FABsin－FAC= ma1 ③
FABcos="mg" ④
联立③、④两式并代入数据得
FAB=5N
FAC="1N"
（2）当a2=10m/s2>a0，此时AC绳不能伸直，F′AC=0。
AB绳与竖直方向夹角a>
据牛顿第二定律
F′ABsina=ma2 ⑤
F′ABcosa=mg ⑥
联立⑤⑥式并代入数据得F′AB=5.7N（5.6N、4
）
考点：此题考查牛顿定律及正交分解法。
智能训练练测考系列答案
，长
的铜棒，用长度也为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中，磁感应强度
．未通电时，轻线在竖直方向，通入恒定电流后，棒向外偏转的最大角度
，求此棒中恒定电流的大小．
，得
.
如右图是“探究求合力的方法”实验示意图.图甲表示在两个拉力F1、F2的共同作用下，将橡皮条的结点拉长到O点；图乙表示准备用一个拉力F拉橡皮条.下列说法正确的是（ ）
| A．甲实验时，两个拉力的大小应相等 |
| B．甲实验时，两个拉力的方向应互相垂直 |
| C．乙实验时，只须使橡皮条的伸长量与甲实验相等 |
| D．乙实验时，仍须将橡皮条的结点拉到O点 |
在广场游玩时，一小孩将一充有氢气的气球用细绳系于一个小石块上，并将小石块静止置于水平地面上，如图所示。风沿水平方向吹，气球受到的风力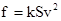
（k是阻力系数，S是迎风横截面积，v是风速）。若水平的风速逐渐增大（设空气密度不变，气球所受的空气浮力不变），则下列说法中正确的是（ ）
| A．细绳的拉力变大 |
| B．地面受到小石块的压力逐渐减小 |
| C．小石块滑动前受到地面施加的摩擦力逐渐增大 |
| D．小石块有可能连同气球一起被吹离地面 |
如图所示，两条电阻不计的平行导轨与水平面成θ角，导轨的一端连接定值电阻R1，匀强磁场垂直穿过导轨平面．一根质量为m、电阻为R2的导体棒ab，垂直导轨放置，导体棒与导轨之间的动摩擦因数为μ，且R2＝2R1.如果导体棒以速度v匀速下滑，导体棒此时受到的安培力大小为F，则以下判断正确的是
A．电阻R1消耗的电功率为 |
| B．整个装置消耗的机械功率为Fv |
| C．整个装置因摩擦而消耗的功率为μmgvcos θ |
| D．若使导体棒以v的速度匀速上滑，则必须施加沿导轨向上的外力F外＝2F |
