题目内容
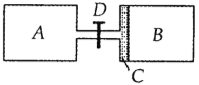
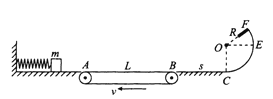
【题目】如图所示,一根轻弹簧左端固定于竖直墙上,右端被质量![]() 可视为质点的小物块压缩而处于静止状态,且弹簧与物块不栓接,弹簧原长小于光滑平台的长度。在平台的右端有一传送带,AB长
可视为质点的小物块压缩而处于静止状态,且弹簧与物块不栓接,弹簧原长小于光滑平台的长度。在平台的右端有一传送带,AB长![]() ,物块与传送带间的动摩擦因数
,物块与传送带间的动摩擦因数![]() ,与传送带相邻的粗糙水平面BC长
,与传送带相邻的粗糙水平面BC长![]() ,它与物块间的动摩擦因数
,它与物块间的动摩擦因数![]() ,在C点右侧有一半径为R的光滑竖直圆弧与BC平滑连接,圆弧对应的圆心角为
,在C点右侧有一半径为R的光滑竖直圆弧与BC平滑连接,圆弧对应的圆心角为![]() ,在圆弧的最高点F处有一固定挡板,物块撞上挡板后会以原速率反弹回来。若传送带以
,在圆弧的最高点F处有一固定挡板,物块撞上挡板后会以原速率反弹回来。若传送带以![]() 的速率顺时针转动,不考虑物块滑上和滑下传送带的机械能损失。当弹簧储存的
的速率顺时针转动,不考虑物块滑上和滑下传送带的机械能损失。当弹簧储存的![]() 能量全部释放时,小物块恰能滑到与圆心等高的E点,取
能量全部释放时,小物块恰能滑到与圆心等高的E点,取![]() 。
。
(1)求右侧圆弧的轨道半径为R;
(2)求小物块最终停下时与C点的距离;
(3)若传送带的速度大小可调,欲使小物块与挡板只碰一次,且碰后不脱离轨道,求传送带速度的可调节范围。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)物块被弹簧弹出,由![]() ,可知:
,可知:![]()
因为![]() ,故物块滑上传送带后先减速物块与传送带相对滑动过程中,
,故物块滑上传送带后先减速物块与传送带相对滑动过程中,
由:![]() ,
,![]() ,
,![]()
得到:![]() ,
,![]() ,
,![]()
因为![]() ,故物块与传送带同速后相对静止,最后物块以
,故物块与传送带同速后相对静止,最后物块以![]() 的速度滑上水平面BC,物块滑离传送带后恰到E点,由动能定理可知:
的速度滑上水平面BC,物块滑离传送带后恰到E点,由动能定理可知:![]()
代入数据整理可以得到:![]() 。
。
(2)设物块从E点返回至B点的速度为![]() ,由
,由![]()
得到![]() ,因为
,因为![]() ,故物块会再次滑上传送带,物块在恒定摩擦力的作用下先减速至0再反向加速,由运动的对称性可知其以相同的速率离开传送带,设最终停在距C点x处,由
,故物块会再次滑上传送带,物块在恒定摩擦力的作用下先减速至0再反向加速,由运动的对称性可知其以相同的速率离开传送带,设最终停在距C点x处,由![]() ,得到:
,得到:![]() .
.
(3)设传送带速度为![]() 时物块能恰到F点,在F点满足
时物块能恰到F点,在F点满足![]()
从B到F过程中由动能定理可知:![]()
解得:![]()
设传送带速度为![]() 时,物块撞挡板后返回能再次上滑恰到E点,
时,物块撞挡板后返回能再次上滑恰到E点,
由:![]()
解得:![]()
若物块在传送带上一直加速运动,由![]()
知其到B点的最大速度![]()
综合上述分析可知,只要传送带速度![]() 就满足条件。
就满足条件。

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目