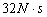题目内容
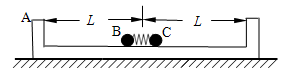
如图所示,质量为M的木块位于光滑水平面上,在木块与墙之间用轻弹簧连接,当木块静止时是在A位置.现有一质量为m的子弹以水平速度υ0射向木块并嵌入其中,则当木块回到A位置时的速度υ以及在此过程中墙对弹簧的冲量I的大小分别为( )


A.υ=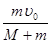 ,I=0 ,I=0 | B.υ=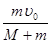 ,I=2mυ0 ,I=2mυ0 | C.υ=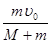 ,I= ,I=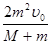 | D.υ=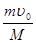 ,I=2mυ0 ,I=2mυ0 |
B
分析:子弹射入木块过程,由于时间极短,子弹与木块间的内力远大于系统外力,故可由动量守恒定律列式求解,子弹和木块的共同速度;然后系统在弹簧弹力的作用下先做减速运动,后做加速运动,回到A位置时速度大小不变,根据动量定理可求得此过程中墙对弹簧的冲量I的大小.
解:子弹射入木块过程,由于时间极短,子弹与木块间的内力远大于系统外力,由动量守恒定律得:
mv0=(M+m)v
解得:v=
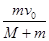
子弹和木块系统在弹簧弹力的作用下先做减速运动,后做加速运动,回到A位置时速度大小不变,即当木块回到A位置时的速度v=
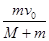 ;
;子弹和木块弹簧组成的系统受到的合力即可墙对弹簧的作用力,根据动量定理得:
I=-(M+m)v-mv0=-2mv0
所以墙对弹簧的冲量I的大小为2mv0
故选B

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的质点从静止开始沿某一方向做匀加速直线运动,它的动量
的质点从静止开始沿某一方向做匀加速直线运动,它的动量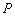 随位移变化的关系式为
随位移变化的关系式为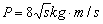 ,则此质点( )
,则此质点( )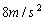
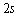 内受到的冲量为
内受到的冲量为