题目内容
4.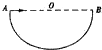 有一半圆形轨道在竖直平面内,如图,O为圆心,AB为水平直径,有一质点从A点以不同速度向右平抛,不计空气阻力,在小球从抛出到碰到轨道这个过程中,下列说法正确的是( )
有一半圆形轨道在竖直平面内,如图,O为圆心,AB为水平直径,有一质点从A点以不同速度向右平抛,不计空气阻力,在小球从抛出到碰到轨道这个过程中,下列说法正确的是( )| A. | 初速度越大的小球运动时间越长 | |
| B. | 初速度不同的小球运动时间可能相同 | |
| C. | 落在圆形轨道最低点的小球末速度一定最大 | |
| D. | 小球落到半圆形轨道的瞬间,速度方向可能沿半径方向 |
分析 根据平抛运动的特点,平抛运动的时间由高度决定,与水平初速度无关
解答 解:A、平抛运动的时间由高度决定,与水平初速度无关,初速度大时,与半圆接触时下落的距离不一定比速度小时下落的距离大,故A错误;
B、速度不同的小球下落的高度可能相等,如碰撞点关于半圆过O点的竖直轴对称的两个点,运动的时间相等,故B正确;
C、落在圆形轨道最低点的小球下落的距离最大,所以运动时间最长,末速度v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$,由于初速度不是最大,故末速度不是一定最大,故C错误.
D、若小球落到半圆形轨道的瞬间,速度方向沿半径方向,则速度方向与水平方向的夹角是位移方向与水平方向夹角的2倍.因为同一位置速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的两倍,两者相互矛盾,则小球的速度方向不会沿半径方向.故D错误.
故选:B
点评 掌握平抛运动的特点,知道平抛运动的时间由高度决定,与水平初速度无关.

练习册系列答案
相关题目
14. 如图所示,一球用细绳系于墙上,绳与墙夹角为θ.球受绳的拉力为F,墙对球的弹力为N,球的重力为G,则( )
如图所示,一球用细绳系于墙上,绳与墙夹角为θ.球受绳的拉力为F,墙对球的弹力为N,球的重力为G,则( )
 如图所示,一球用细绳系于墙上,绳与墙夹角为θ.球受绳的拉力为F,墙对球的弹力为N,球的重力为G,则( )
如图所示,一球用细绳系于墙上,绳与墙夹角为θ.球受绳的拉力为F,墙对球的弹力为N,球的重力为G,则( )| A. | F和N相等 | B. | F一定小于G | ||
| C. | F、N大小之和等于G | D. | F、N、G三力平衡 |
15.学校举行的运动会上,下列哪些项目注重位移的大小( )
| A. | 三级跳远 | B. | 4×100m接力赛 | C. | 铅球 | D. | 标枪 |
12.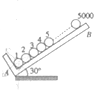 如图所示,5000个大小相同、质量均为m且光滑的小球,静止放置于两相互垂直且光滑的平面A、B上,平面B与水平面的夹角为30°,已知重力加速度为g,则笫2014个小球对第2015个小球的作用力大小为( )
如图所示,5000个大小相同、质量均为m且光滑的小球,静止放置于两相互垂直且光滑的平面A、B上,平面B与水平面的夹角为30°,已知重力加速度为g,则笫2014个小球对第2015个小球的作用力大小为( )
 如图所示,5000个大小相同、质量均为m且光滑的小球,静止放置于两相互垂直且光滑的平面A、B上,平面B与水平面的夹角为30°,已知重力加速度为g,则笫2014个小球对第2015个小球的作用力大小为( )
如图所示,5000个大小相同、质量均为m且光滑的小球,静止放置于两相互垂直且光滑的平面A、B上,平面B与水平面的夹角为30°,已知重力加速度为g,则笫2014个小球对第2015个小球的作用力大小为( )| A. | 1493mg | B. | 2014mg | C. | 2015mg | D. | 2986mg |
16.将一杯热水倒入盛有冷水的容器中,冷水的温度升高了10℃,再向容器内倒入一杯相同质量和温度的热水,容器中的水温又升高了6℃.如果继续向容器中倒入一杯同样的热水,则容器中的水温会升高( )
| A. | 5℃ | B. | 4℃ | C. | 3℃ | D. | 2℃ |
13.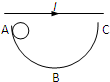 在一水平通电直导线的正下方,有一半圆形光滑圆弧轨道,一导体圆环自轨道左侧的A点无初速度释放,则下列说法中正确的是( )
在一水平通电直导线的正下方,有一半圆形光滑圆弧轨道,一导体圆环自轨道左侧的A点无初速度释放,则下列说法中正确的是( )
 在一水平通电直导线的正下方,有一半圆形光滑圆弧轨道,一导体圆环自轨道左侧的A点无初速度释放,则下列说法中正确的是( )
在一水平通电直导线的正下方,有一半圆形光滑圆弧轨道,一导体圆环自轨道左侧的A点无初速度释放,则下列说法中正确的是( )| A. | 圆环能滑到轨道右侧与A点等高处C | B. | 圆环中有感应电流产生 | ||
| C. | 圆环最终停在轨道的最低点B | D. | 圆环运动过程中机械能守恒 |
14.在地球大气层外有大量的太空垃圾.在太阳活动期,地球大气会受太阳风的影响而扩张,使一些原本在大气层外绕地球飞行的太空垃圾被大气包围,从而逐渐降低轨道.大部分太空垃圾在落地前已经燃烧成灰烬,但体积较大的太空垃圾仍会落到地面上,对人类造成危害.以下关于太空垃圾不正确的说法是( )
| A. | 大气的扩张使垃圾受到的摩擦阻力而导致轨道降低,势能不断减小 | |
| B. | 太空垃圾在与大气摩擦过程中机械能不断减小 | |
| C. | 太空垃圾在轨道缓慢降低的过程中,由于与大气的摩擦,速度不断减小 | |
| D. | 太空垃圾在轨道缓慢降低的过程中,向心加速度不断增大而周期不断减小 |
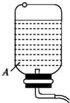 如图所示,倒置的饮料瓶内装着水,瓶底开有一小孔,瓶塞内插着一根两端开口的细管,其出水口水平,从水平出水口射出的水在空中形成弯曲的细水柱,它显示了水做平抛运动的轨迹.将它描在背后竖直放置的纸上,再进行分析处理.现仅有一盒钢卷尺,请你粗略地得出水流出管口时的速度大小和从管口到地面之间的空中的水柱的质量(已知水的密度为ρ,重力加速度为g).
如图所示,倒置的饮料瓶内装着水,瓶底开有一小孔,瓶塞内插着一根两端开口的细管,其出水口水平,从水平出水口射出的水在空中形成弯曲的细水柱,它显示了水做平抛运动的轨迹.将它描在背后竖直放置的纸上,再进行分析处理.现仅有一盒钢卷尺,请你粗略地得出水流出管口时的速度大小和从管口到地面之间的空中的水柱的质量(已知水的密度为ρ,重力加速度为g). 如图所示,在利用重物自由下落“验证机械能守恒定律”的实验中,打点计时器所用电源频率为50Hz,实验要求打点计时器在打第一个点时释放纸带.甲、乙、丙三个学生分别用同一装置各打出一条纸带,量出各纸带上第1、2两点间的距离分别为0.48cm,0.19cm和0.18cm,肯定其中一个学生在操作上有错误,该同学是甲.其错误的操作是先释放纸带再接通电源.
如图所示,在利用重物自由下落“验证机械能守恒定律”的实验中,打点计时器所用电源频率为50Hz,实验要求打点计时器在打第一个点时释放纸带.甲、乙、丙三个学生分别用同一装置各打出一条纸带,量出各纸带上第1、2两点间的距离分别为0.48cm,0.19cm和0.18cm,肯定其中一个学生在操作上有错误,该同学是甲.其错误的操作是先释放纸带再接通电源.